数学教学过程化的策略

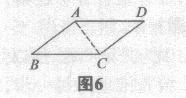
　　由上面的操作过程，学生会发现，如图6，在四边形ABCD中，已知AB=CD，且BC＝AD，要证明四边形ABCD是平行四边形，只需连接AC，并证明△ABC与△CDA全等即可．这个证明思路就是在拼接三角形纸片的过程中发现的．
　　

　　在数学性质、定理的教学中，要把重点放在引导学生探究性质和定理的发现过程、证明思路的猜测过程和证明方法的尝试过程上，以避免出现学生所反映的“老师添设辅助线总是‘马到成功’，演算证明总是简捷又灵活”，“我们是一听就懂，但一做题就错(或不会)”的现象．
　　
　　策略4：引导学生参与综合实践活动
　　
　　新课改重视让学生参与综合实践活动，让学生运用自己已有的知识和经验，经过自主探索和合作
　　
　　交流，解决与生活经验密切联系、具有一定挑战性的问题，以发展他们解决问题的能力．例如，在学习了全等三角形的知识后，可以引导学生实地测量不能到达的两点之间的距离；在学习了相似三角形的知识后，可以测量某座高楼的高度；等等．
　　
　　进行综合实践活动，不同于直接解答给定的问题，综合实践活动用的时间比较长，它是一种具有现实性、问题性、实践性、综合性和探索性的学习活动，一般分为以下3个阶段：
　　
　　(1)进入问题情境阶段；
　　
　　(2)实践体验阶段；
　　
　　(3)解决问题阶段．
　　
　　这就要求学生必须参与以上3个阶段的全部过程，而不是只参与其中的某些环节．
　　
　　案例4调查某校八年级学生的视力情况．
　　
　　此案例安排在学完统计的有关知识之后进行，要求学生利用统计的有关知识，通过调查学生的视
　　
　　力情况，作出判断，提出改进建议，从而培养学生的统计意识．指导学生调查时，要以学生亲身经历和体验统计过程为主线，引导学生发现并提出问题，用适当的方法收集和整理数据，用合适的图表展示数据，对数据做简单的分析，并对自己的分析、思考进行交流和改进．
　　
　　综合实践活动中，应让学生参与调查的全过程，仔细分析这个问题可以发现，这个调查活动应分为“提出问题一收集、整理数据一分析判断”3个阶段进行．
　　
　　(1)提出问题．
　　
　　综合实践活动的第一步(进入问题情境)，对本案例而言就是明确活动的目标，提出具体的问题．
　　
　　这个案例的目标非常明确(调查某校八年级学生的视力情况)，范围也相对较小(在某学校八年级
　　
　　学生中进行调查)，方法有两种：一是普查；二是抽样调查．如果该校八年级学生不是很多，可以采用普查的方法．如果学生较多，可以采用抽样的方法，这时应提醒学生注意样本选取的代表性和适当的样本容量．
　　
　　通过组织学生讨论，决定采取抽样的形式进行调查，为了便于记录和统计，很容易想到设计一个记录表(如下页表1)：
　　
　　(2)收集、整理数据．
　　
　　综合实践活动的第二步(实践体验)，对本案例而言就是具体调查，把调查过程中得到的数据收集
　　
　　起来并加以分析．从该校八年级学生中随机抽取了50名学生进行视力检查，收集到了100个数据(具
　　
　　体数据略)，把这些数据填在表l中，为了便于分析，对这100个数据进行简单的统计汇总．
　　
　　①右眼情况：视力是0.1的1人；视力是0.2的1人；视力是0.3的2人；视力是0．4的2人；视力是0.5的2人；视力是0.6的3人；视力是0.7的4人；视力是0.8的5人；视力是1.0的9人；视力是1.2的10人；视力是1.5的11人．
　　
　　②左眼情况：视力是0.1的1人；视力是0.2的2人；视力是0．3的1人；视力是0．4的5人；视力是0.5的3人；视力是0.6的5人；视力是0.7的2人；视力是0.8的4人；视力是1.0的10人；视力是1.2的7人；视力是1.5的10人．

上一页 [1] [2] [3] [4] [5] 下一页