道理.无奈之下,我脱口而出:可以合并的项就是同类项!说完了又后悔了,这算什么定义?犯了循环定义之大忌,如同说“长了猪毛的动物是猪”一样.但是,这样的说法,是不是更能让学生去体会同类项的“意”呢?
由此可见,有些概念,我们不能过于纠缠于其定义表述是否“严谨”,而应把着力点放在学生对概念内涵的理解上,也就是数学的“意”的体味.
定理法则
定理的证明其作用有时往往不亚于定理内容本身,而法则也有其合理性.但如何证明和理解定理和法则,有不同的方法.帮助学生理解其“意”,是关键所在.
全等判定,为什么没有“SSA”?
对于这个问题,教者往往通过举一个反例说明,简捷而符合逻辑.其实,如果构造出图1,线段AB和∠B大小不变,线段AD绕着点A旋转,通过动画演示可以看到,当AD>AE(AE为点A到直线BC的垂线段)时,与直线BC交于两点M、N,△ABM和△ABN满足条件“SSA”,但不全等.其本质原因就在于边AD可以绕着点A“旋转”.随着线段AD的大小变化,可以看到,其“旋转”产生了不同的结果.如,当AD=AE时,AD无法“旋转”,与BC只有一个交点,于是“HL”可以作为全等的判定.而当AD≥AE时,线段AD“旋转”与射线BC(不包括点B)只有一个交点,此时“SSA”可以作为全等的判定.而当AD<AE时,由于线段AD与直线BC没有交点,不能构成三角形,因此,不能形成全等的判定.
通过这个过程,学生不但理解了为什么没有“SSA”的全等判定,而且知道了全等判定“HL”和“SSA”的内在联系,以及“SSA”可以作为全等判定的条件.这一过程,学生不必用文字去表述,达“意”即可.
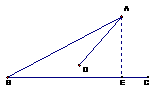
图1
多边形外角和定理:多边形的外角和为360?
其证明方法有多种,怎样才能理解其本质?不妨把多边形浓缩成一个点,让我们绕着这个点旋转一周,便回到原来的状态,而“旋转一周”之“意”,学生便理解了多边形的外角和为360埃比唬獠荒芴娲ɡ淼闹っ鳎荒茏魑ㄖ侄危由疃远ɡ淼睦斫猓?/SPAN>
负负得正.
这个法则无论是用“反方向运动”,还是用“借进借出”,学生理解起来都很别扭.而形式化的证明更不可能.对于初一学生,更重要的是运算,考虑到学生的“量力性”,不加选择地要求学生知道“为什么”是不合适的.既然如此,何不处理得简单一些?比如“开关”原理,开关两次才能回到原来的状态,学生很容易记住.
需要说明的是,笔者并不崇尚这种并不严谨的教学,而是认为在一定的教学阶段可以采取这种方法,或者作为补充理解的手段.随着学习的进一步深入,往往有必要作数学化解释.
解题教学
数学习题有些可以纯粹模仿,依据某些固定程式,按部就班就能解答.如,合并同类项、解一元一次方程等.而有些习题的解答,似乎都有规律可循,但却无法程序化.我们常常有这种体会,突然间一种优美的解题方法出来了,连自己也吃惊.至于这种思路怎么产生的,我们自己也说不清,这种数学之“意”,无法直接传授给学生.
在一次数学习题课上,笔者抛出了这样一题:
如图2,正方形ABCD的边长为2,点E在AB边上,四边形EFGB也为正方形,设△AFC的面积为S.则()
A.S=2B.S=2.4C.S=4D.S与BE长度有关
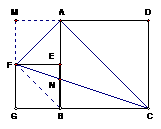
图2
上一页 [1] [2] [3] 下一页
