>
笔者没有立即“启发”,也没有“循循善诱”地引导学生解题,而是留出了足够的时间让学生去独立思考.并提出了这样几个要求:
1.至少给出一种解法;
2.尽可能多地想出多种解法,并对这些解法进行比较,哪一种解法更简捷?
3.你是如何利用题中信息的?
4.你是怎么想到这些解法的?
在随后进行的交流中,学生先后给出了如下思路:

笔者没有急于引导学生去发现FB∥AC,而是给学生提供更多、更宽泛的发散思维的机会,从而得到了丰富多彩的证明方法.通过比较反思,学生才能更多地体会到数学的“意”,积累更多的解题经验.奇怪的是,发现思路6这一简单证法的,并不是数学学习厉害的,而是一位数学中下水平的同学.通过了解得知,更多的学生在计算面积时按常规思路:直接计算或割补法,发现不便于直接计算,所以选择割补法.出现这一想法,显然是由于大量解题后的经验积累.而想到思路6的同学,并无明显的这种经验积累的痕迹,只是看出图中FB好像和AC平行,发现很容易证得.可见,过多的解题方法的总结,可能在解题时造成先入为主的现象,从而窒息或者窄化数学的“意”.这种现象在另一道习题的解答中也有反映.
如图3,四边形ABCD和EFBG都是矩形,是否存在这样的直线,把这个图形的面积两等分?如果存在,有多少条?
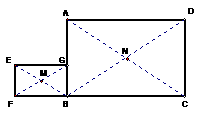
图3
由于刚刚学过矩形,很多学生立即想到矩形的中心对称性质,得到直线MN能把图形面积两等分.同样是一个数学成绩一般的学生不假思索地说:无数条.他的理由是,把一条直线从任意方向平移,把图形面积分割成两部分,这两部分的面积总会有由小到大,由大到小的过程,而这中间必然有相等的可能.这样的直线由于方向可以任意放置,所以有无数条.这样的解答过于直观,貌似不太严密.但这种数学的“意”确实珍贵,值得注意和保护.
数学教学中,我们固然要重视显性的,可表述的数学经验和方法,但也不能忽视不可言传的“意”.而这种数学之“意”的形成一般不是靠教者言传或示范,而是靠学生通过丰富多彩的学习的过程去形成,这样才能到达得“意”而忘言的境界.
正如老子所言:“道可道,非常道”[3].
参考文献:
1.冯友兰,中国哲学简史,[M].天津社会科学院出版社,2005.10:11.
2.杨柳桥,庄子译注,[M].上海古籍出版社,2006.11:214~215.
3.陈国庆、张爱东译注,道德经,[M].三秦出版社,1995.8:1.
上一页 [1] [2] [3]
