问题一:根据横行的数字规律,第七行的数字是哪些呢?
问题二:请计算(a+b)2,(a+b)3,(a+b)4
问题三:根据问题二的规律你能直接写出(a+b)6吗?
通过对《杨辉三角》来经历探究公式的过程,从中激发学生学习数学的兴趣。
案例四:九年级(上)二十二章第3节《实际问题与一元二次方程》后有一篇选学内容《发现一元二次方程根与系数的关系》。我们也可将它的内容作为学生探究问题的素材。
问题:解下列方程,将得到的解填入下面的表格中,观察表格中两个解的和与积,它们和原来的方程的系数有什么联系?

探索2:如果一元二次方程的二次项系数不是1,你又能发现什么规律?
三、将“选学内容”演变为反思问题的切入口
知识、能力和创新三者应水乳交融,交融的基础是过程,反思则是过程的重要环节。学生在反思中补充和完善自己的知识结构,获得了解决问题的策略。因此,教师应及时抓住契机,引导学生反思能否从另外角度或途径去分析、思考,从而寻找多种方法求解,寻找最佳解题方案,并在解决问题过程中鼓励学生提出新的问题,使材料成为问题的“策源地”和“催化剂”。使学生的思维朝着灵活、精细和新颖的方向发展。
案例五:《勾股定理》是几何中一个非常重要的定理。其证明方法多种多样,且每种方法的背后都隐含着一定的知识点,学生理解起来较为困难。在学习八年级(下)第十八章第1节《勾股定理》后,我们可以结合后面的选学内容《勾股定理的证明》加以设计,使学生对这一定理得到了更深刻的理解与认识。
问题一:我们知道,勾股定理反映的是直角三角形三条边之间的关系:a2+b2=c2。
下面介绍几种证明勾股定理的图形,你能根据这些图形及提示证明勾股定理吗?
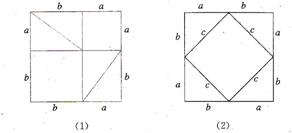
1、传说中毕达哥拉斯的证法(图1):
提示:(1)中拼成的正方形与(2)中拼成的正方形面积相等。
2、弦图的另一种证法(图2)
提示:以斜边为边长的正方形的面积+四个三角形的面积=外正方形的面积。
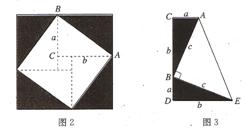
3、美国第20任总统茄菲尔德的证法(图3):
提示:三个三角形的面积和=一个梯形的面积。
问题二:除上述的几种证法外,你能尝试其他的证法吗?
证明勾股定理的方法有很多,你若有兴趣可从有关书籍或互联网上找到一些证明方法,读懂它,并与同学相互交流。
经过对此题多种证法的反思,学生扩大了知识面,开阔了视野。
案例六:在学习了九年级第二十七章后,我们可以结合第二十二章,对选学内容《黄金分割数》加以设计。

我们知道五角星是常见的非常美丽的图形,其原因是在五角星中可以找到所有线段的长度关
问题三:我们把
上一页 [1] [2] [3] 下一页
