数学教师教学知识的结构与特征

1)教学规定的维度：教学大纲，相应的教材和教学参考书，这些文献所涉及的知识；
　　
　　(2)教学目标的维度：对活动目标的分析，关心它能够推动什么，思考学生在活动中应该得到哪些方面的发展；
　　
　　(3)数学的维度：与活动相关的数学知识，如课例1，需要进行数学推理，推理中所用的概念，定理与性质，推理的数学表述，数学活动过程的记录；
　　
　　(4)教学法的维度：与他人一起学习，在数学活动中，班级、小组构成小社会，师生交流，相互争论，教学相长．
　　
　　由课例l可见，教师要从多方面考虑设计数学活动，需要把各种各样的知识与能力有机结合起来，从而说明教师数学教学知识的多样性与综合性．
　　
　　三、数学教学知识的实践性与综合性
　　
　　以下提供的教学课例，用以说明教师对两个不同学生小组的引领，看到教师对学习活动的指导作
　　
　　用，在教学中教师对行动作出各种调整．以下用不同年级、不同内容的教学课例，说明数学教学知识的特征．
　　
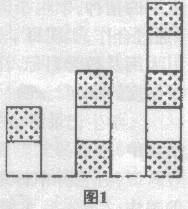
　　课例2(初一)教室里有两堆不同颜色的单位小立方块．教师让学生小组考虑：利用这小立方块可以堆砌高度一定的不同的塔．这些塔是用白色或黄色方块构建的，同颜色的两个方块不能堆叠在一起，每个小塔的底部只放一个方块．学生使用方块做尝试、教师问：
　　
　　·如规定小塔有五个方块高，可以构建多少座不同构成的小塔?如规定小塔有六个方块高，可以构建多少座不同构成的小塔?
　　
　　·是否可以找到构建塔数的规律和方法?解释你是怎样想到的．
　　
　　小组A学生根据问题进行工作，一些问题迅速呈现出来：
　　

　　(1)与任务相关问题的约束条件：罗伊推动学生重述没有同颜色的方块能够堆叠在一起(但是除去这个条件后，再让学生说明约束条件对解题的限制)，重新解决约束条件的问题．
　　
　　(2)提出有关塔的对称性的相关问题：有学生问，如果塔的颜色依次为白白白白黄，是否等同于黄白白白白?罗伊建议想象一个真正的塔，其底层涂了黄色或白色，他问：“如果我们在每个不同的水平上涂色，我们是否得到同样的塔?如果你说是或否，说出你的理由．”
　　
　　(3)有关只用一种颜色构建塔的可能性的问题，罗伊问他们：“如何看待这些塔要满足题日的条件，即同颜色的方块不能堆叠?”
　　
　　小组B有些学生欣赏从较小的塔人手的想法．某些小组开始明确叙述一个模式，并开始说明对于任意高度所能构建的符合条件的塔的个数．经过一段时间合作努力，小组得到较简单情况下的结果．如下表．
　　

　　经过讨论，学生达成了一些共识：
　　
　　·当高度是l到6时，所构建的塔都有两种模式；
　　
　　·当高度是2以上时，塔的模式都是两色相间的；
　　
　　·高度是3，5，7等奇数时，一种颜色方块数日是奇数，另一颜色方块数目是偶数；
　　
　　·高度是2，4，6等偶数时，构成塔的两种颜色的方块数目相等．
　　
　　还有一些意见是非数学的，例如有学生指出，“塔不能太高，否则塔就站不稳了．”
　　
　　开始时，学生对问题的处理是发散的，而教师的即时处理必须是根据课堂活动的具体情况机灵
　　
　　而有创意．在教师的指导下，学生倾向于注意约束条件，例如，规定从底层是一个方块开始，这样上面每一层也只放一个方块．教师的教学处理不能预先设定，而要根据活动的具体进展“见机行事”，比较各组学生的情况，有针对性地进行．
　　
　　什么是“见机行事”?没有必要做具体的解释，教师在教学中的现场扮演，是对学生在活动中的具体处理的及时应答．
　　
　　·

上一页 [1] [2] [3] [4] [5] 下一页