数学教师教学知识的结构与特征

这种“在行动中扮演”就好比下棋，看学生如何做，教师要先读棋，再应答．棋子支配着罗伊分析学生思维中的有关因素．例如，B组在开始概括模式时遇到困难，罗伊建议从简单情况开始．又如出现同色两方块相邻时，教师让A组重述问题的约束条件．这种读懂学生的思维表述，在一定的程度上是罗伊回答学生问题的标准．学生的行动是受一定的思维所支配的，教师应该关注学生的问题、解法、困难以及应对问题的途径．
　　
　　·这种“见机行事”，涉及做事的方式．例如罗伊应答组A的关于塔的对称性问题，他建议学生考虑颜色的顺序，使得能够按照相同标准处理．
　　
　　·这种“见机行事”涉及教帅教学的重要方面，这就意味着，教师通过适当的问题，让学生鉴别他们的解答．这里也隐含师牛交流各自数学观点以及解决问题的方法．
　　
　　从课例2可见，数学教师的教学知识，主要是在教学中产生，并在教学中得到检验和强化．在教
　　
　　学中所用到的知识，往往不局限于某个章节的知识，而是与数学其他分支，其他学科的知识综合交
　　
　　织在一起的．对于课例1，用到了四个维度的知识；对于课例2，教师要用到排列组合的准备知识，数的奇偶性知识，重心与平衡的知识，模式与结构的知识，等等．在教学中所用到的知识，也不局限于数学内容的知识，还包括动手实践，探索发现，从简单到复杂，从特殊到一般等科学认识沦和方法论的原理．
　　
　　四、对学生解答的感知与教学决策
　　
　　对学生的关心与理解，是正确教学决策的前提，也是课堂教学有魅力的保证．下课前二十来分
　　
　　钟时，罗伊要求学生写出他们的问题和解答，他在班内巡视，看学生正在做什么，这涉及选取的策略
　　
　　和所用的理由．课后，他选出某些解答，第二天提供其他学生小组分享．这些选用的解答是对或者错?
　　
　　哪些解题策略能在类似的情况下优先使用?迅速引起其他学生思考．他从中选出一个想法与众不同的学生向全班介绍．事实上，罗伊倾向于请出不同学生，他认为，如果所请的学生过于集中，有时会引起负面效果．
　　
　　这是教学决策另一个关键方面：让人人享有平等的机会，让机敏而新颖的见解得以传播，让误解及时得到澄清；让人人学有所得，为后续教学的再投资留下伏笔．
　　
　　课例3对学生问题的再投资(高二)
　　
　　在一个国际活动中，来自不同国家的10位代表第一次见面，他们两两握手做自我介绍．试问：(a)在这次见面中有多少次不同的握手?(b)如果代表的人数多于10人，共有多少次握手?对于任意人数赴会，能否找出一种办法计算不同的握手次数?(这问题和我国高中数学选修系列2—3课本第28页例3实质是一样的．)
　　
　　教师让学生回忆该问题，有学生说很容易，罗伊认为这太好了，因为他想看到学生各种各样的具体的思路，而不仅仅是答案．
　　
　　第一小组受邀上台，卡拉与克罗蒂亚到讲坛上出示答案，他的答案是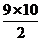

=45．对于第二个问题，卡拉解释说：例如，不妨设有20人，必须握手20×19次，再除以2．教师问为什么要除以2？卡拉
　　
　　回答说：甲乙握手与乙甲握手是一样的，故要除以2．问题似乎已经解决，但教师还希望扩大收获，此
　　
　　时恰有另一个学生伯纳发问：
　　
　　为什么10个人得到45次握手，20人得到190握手呢?罗伊发动班里展开讨论，并且问：“你们是
　　
　　怎样想的?”两个互相矛盾的观点呈现在同学面前．
　　
　　伯纳：“计算是错误的，因为如同10人的情况，你必须考虑到这样的事实，握手的次数是随着人数的减少而减少的．”
　　
　　巴卡尔：“对于20人，应该两倍乘以l0人的握手数，因此答案是90而不是190．”
　　
　　罗伊要求学生考虑5人的情况：“我们应该如何处理?是不是该握手22．5次?”，有学生提出答案应该是握手15次，卡拉提出握手次数不可能是22．5··…·
　　

上一页 [1] [2] [3] [4] [5] 下一页