数学教师教学知识的结构与特征

　　问题源于组合计数的章节，伯纳的见解含有正确的成分，就是“人数越少，握手次数也少”；然而，他把握手次数)，与人数n的关系误解为正比例关系，而实际不是如此．
　　
　　教师巧妙的设问以及所使用的反例，正是引导学生走出认知误区的亮点．
　　
　　有学生指出y=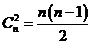

，而伯纳误以为y与n是正比例关系，这正是一种误解．教师及时理解学生进入数学误区的原因，这是本课例取得成功的关键．教师要求学生们判断伯纳的想法是否正
　　

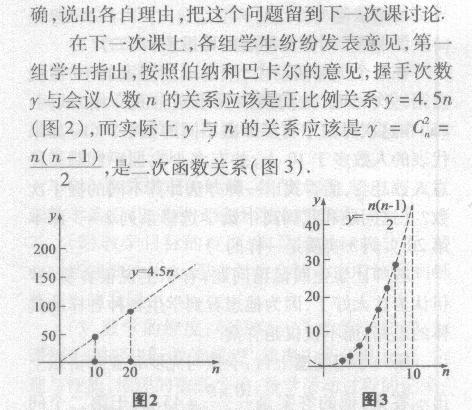
　　第二组同学指出，握手的次数不可能是22．5，因为握于次数是正整数，第一组所说的二次函数的定义域还应该是离散型的集合(图3)，因为赴会人数n也是正整数．
　　
　　教师及时作了总结，同学们通过合作学习，把组合问题与二次函数联系起来，义把连续型函数与离散型函数区分开来，我们的学习有了，新的收获．
　　
　　这可见到教师在教学中各种各样的扮演，在教育的水平上，罗伊把学生的问题抛回给学生分
　　
　　享，引导他们负责任地提出有效的解答．(在这里我们再次看到他坚持让学生进行说理．)在数学的水
　　
　　平上，罗伊找出并提供反例，“如果是5人的情况，是否握手22．5次?”刚这个反例，反击“加倍”的策略．这种反例也是对学生引导的策略，这种策略具有教育的意图，因为罗伊的日的是引导学生反思自己的解答，推动并激发学生产生疑问．
　　
　　五、问题的突发性与应答的机敏性
　　
　　前面的课例，讨论了教师数学教学的知识有三个基本特点：
　　
　　(1)它的性质接近于在行动中的知识，一个“见机行事”更甚于实际的知识；
　　
　　(2)它的情境特点：它与课堂出现的问题，以及解决问题的思路紧密相连；
　　
　　(3)学生问题的出现具有不可预知性，新课程要求教师能及时跟踪学生的想法，要恰当地引导学生走出误区，教师必须有较高的知识水平与较强的引领能力．
　　
　　数学教师在他们的教学中所从事的情境，在方法上与数学家大不相同．以上的课例说明了这些差
　　
　　异．在对问题的探索中(例如计算塔的个数问题)，一个数学家肯定把注意力集中在组合模型，寻找一般的公式，找出所有可能的塔数．在其中要规定各种各样的约束条件(不同的颜色，不同的安排，等等)．教师在实际教学中处理这个问题时，就会从不同的视觉进入．他会联系到学生，联系到学牛各种各样的策略，联系到自然产生的模型，教师会根据这个模型，对问题及其各种解法进行再投资．如同课例2，教师不仅对排列组合模型感兴趣，更对学生自然产生的模型，他们所陈述的道理，这些理由的有效性，以及他们所取得的进步感兴趣．
　　
　　数学教学知识总是在教与学的线索中得以建立，得到解释．设计教学情境，同时用到了各种各样的知识来源，包括教育的，教学法的，数学的甚至是规定性的．这些维度不足一成不变的．数学思想
　　
　　方法的渗透是潜移默化的，关键是对学生情况的理解．课堂中的数学情境，总是把求解、探索结合在一起，各种因素综合交织．各种因素不会单独地扮演，它们总是相互影响，相互选择，联袂演出．
　　
　　在上述教学实践中所需要的知识，即使称之为教师的为教学的数学知识，也永远不是纯数学知识．它是各种知识的交织与组合，是非常特殊的知识．
　　
　　数学课堂教学，教师的职业活动，建构知识在教学中的切入点，指导着教师在教学中的扮演．
　　
　　这些知识通过其他活动得以发展和提炼，对学生发挥引领作用．这是近来研究教师教育实践的新线
　　
　　索，也是教师职业发展的新趋势．教师的感悟在实践中生成，它是动态发展的知识，它既相对独立实践，又在实践中逐步形成其意义．
　　
　　参考文献
　　

上一页 [1] [2] [3] [4] [5] 下一页