初中数学精心设计问题串 提高课堂教学效益 |
|
|
| 来源:不详 更新时间:2012-11-22 12:11:34 |
|
|
|
|
5x-3=0,3x2+20x-7=0的两个根与两根之和、两根之积,观察方程的根与系数有什么关系?
问题3你能猜想出方程ax2+bx+c=0(a≠0)的两根之和与两根之积是多少吗?观察方程的根与系数有什么关系?
问题4这个规律对于任意的一元二次方程都成立吗?如方程x2+x+1=0,它的根也符合这个规律吗?
问题5请你用数学语言表达上述规律.
点评在解答这些问题的过程中,通过问与问之间的层层推进,引导学生按照一定的逻辑顺序层层深入,由易而难,由外而内,由现象到本质,由特殊到一般,学生在解决这些问题的过程中,对一元二次方程的根与系数的关系的掌握也基本系统化了.
案例3“平行四边形的判别”的教学
问题1你能在平面内用两对长度分别相等的小木棒首尾顺次相接组成一个平行四边形吗?说说你是怎么操作的,画出图形并说明理由.
问题2你能将两根长度相等的小木棒放置在有横条格的练习本的纸上,使得两根小木棒的端点所代表的四个点能在纸上画出一个平行四边形吗?说说你是怎么操作的,画出图形并说明理由.
问题3你能用这两根长度不等的绳子放在有横条格的练习本的纸上,使得两根绳子的端点所代表的四个点能在纸上画出一个平行四边形吗?说说你是怎么操作的,画出图形并说明理由.
问题4通过以上三个问题,你能得出哪些结论?
点评这个例子中,问题1、问题2、问题3这三个问题中,每个问题都要求学生经历操作实验、
数学验证、概括总结三个阶段,因此,每个问题都包含一组有序的问题串,而问题1、问题2、问题3这三个问题实际上也组成了一组更大的有序的问题串,学生通过对二个问题的操作、实验、猜想和探索研究等活动,自主获得了平行四边形的三个主要的判别方法,也使学生真正参与到教学活动中去.这样充分体现了问题的层次感,也更适合学生探究.
三、用问题串解决问题
运用问题串进行教学,实质上是引导学生带着问题(任务)进行积极地自主学习,由表及里,由浅入深地自我建构知识的过程.因此,问题串的设计应体现梯度性和过渡性,备课时要在精细化上下工夫,使学生在问题串的引导下,通过自身积极主动的探索,实现由未知向已知的转变.
案例4“抛物线与三角形的面积”的复习教学
已知:如图2,抛物线y=x2-2x-4与直线y=x交于A,B两点,M是抛物线上一个动点,且在直线AB的下方,连接OM.
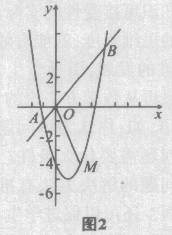
问题1当M为抛物线的顶点时,求△OMB的面积.
问题2(根据2005年湖北省武汉市中考卷第40(2)题改编)
当点肘在抛物线对称轴的右侧,且△OMB的面积为10时,求点M的坐标.
问题3(根据2008年广东省深圳市中考卷第22(4)题改编)当点M在抛物线对称轴的右侧,点M运动到何处时,△OMB的面积最大?
问题4(根据2008年安徽省芜湖市中考卷第24(3)题OM与直线AB相切时,求点M的坐标.
点评这是一道基础题和三道中考改编题的整合.其中问题l(已知三角形的3个顶点坐标,求它的面积)是一道常规问题,学生比较熟悉,人手相对容易,同时也为后面问题的探索做好铺垫,起到“脚手架”的作用;问题2是问题1的逆问题,让学生在抛物线上找满足条件的点M;问题3是在动态过程中求三角形面积的最值,同前2个问题相比,对学生的思维有着更高的要求;问题4是问题2的变式,它改变了问题的呈现方式,突出了对学生进行问题本质的训练,要求学生具有较高的模式识别能力.这四个问题有着很强的整体性,不但突出了问题的层次性,一步一个台阶,逐步深人递进,而且
体现r方法的迁移性,并始终强调三角形面积的求法.同时,问题的层次性也满足了不同层次学生的
上一页 [1] [2] [3] [4] 下一页
|
上一个数学: 数学教师教学知识的结构与特征
下一个数学: 高中数学破题技法之转换开门 亦必亦充 |
|
|
|
|
|
|
