让平面几何题更加生动活泼

作者：刘明辉
　　
　　对当前的初中平面几何课程的改革，我们至少有以下三点认识：第一，平面几何教学要选取现实的、有意义的、富有挑战性的内容，紧紧与学生的生活经验与活动经验相联系，为学生提供生动的几何背景；第二，几何的学习方式应该包含观察、实验、猜想、证明等多种形式的数学活动；第三，初中平面几何课程应该兼顾培养学生的演绎推理和合情推理两种能力，从改进以往传统的几何教学目标的角度看，当前尤其需要加强合情推理能力的培养．概括起来，本次初中平面几何课程改革的着眼点在于：不是把平面几何课程当作一系列现成的、凝固的、经典的知识体系去让学生接受，而是把它作为一个可以动态生长的知识领域让学生去探究．在这里，我们探讨传统平面几何题的升华，这既是新课程改革带来的理念的注入，也是来自中学数学教育工作者发自内心的创新和探索，它对新课程平面几何的教学是大有裨益的．
　　
　　一、让背景“活”起来——应用式升华
　　
　　传统的平面几何题一般都过于平淡、缺乏生活气息．如果对其赋予与学生密切相关的生活情境，不仅可以激发学生的参与热情，而且还有强烈的教育意义．
　　
　　例l：如图1，△．ABC是一个钢架，AB=AC，AD是连接A与BC中点D的支架．求证：AD上BC．
　　

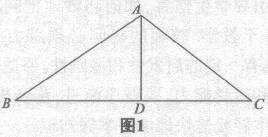
　　例2：如图1，△ABC是一个房屋的人字梁，其中AB=AC，为了使人字梁更加稳固，房主要求小木工在顶点A和横梁BC之间加一根柱子AD．可小木工由于未学过几何，不知榫眼D该凿在BC何处，才能使AD⊥BC．请问你能帮助他吗?写出方案并说明理由．
　　
　　点评：例2是由一个传统题如例l升华为应用性的问题，与例1相比，例2的优越性在于：首先，题型开放了．有的学生凭直觉人胆猜想D为BC的中点；也有的学生依赖生活经验，用悬挂铅垂线的方法寻找D点(铅垂也可用小石块代替)；还有的学生想到先拉根细线，再用三角板靠，等等．其次，背景活了．创设“小木工由于未学几何以至不会画图”的情境，不仅可以激发学生学习几何的兴趣，同时也教育学生：学好几何是何等重要!】
　　
　　二、让题型“活”起来——开放式升华
　　
　　把过去传统几何题的证明结论，升华为猜想发现结论；或寻找条件部分，然后证明，由封闭向开放转化．
　　
　　例3：如图2，△ABC为等边三角形，点D、E分别在BC边和CA边上，BD=2DC，CE=2EA，．AD与BE相交于G．求证：AD=BE
　　

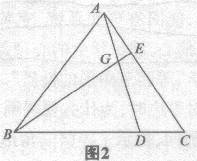
　　例4：如图2，△ABC为等边三角形，点D、E分别在BC边和CH边上，．BD=2DC，CE=2EA，AD与BE相交于G，试就有关图形的形状、大小和关系得出尽可能多的结论．
　　
　　【点评：传统题例3隐去结论“求证AD=BE”，就升华为开放题例4．结论是多种多样的，学生不同的思维方式、不同的数学认知结构和不同的数学能力，可能出现不同的结果．如先考虑三角形的全等关系，有(1)△ACD≌△BAE；由此可推出，(2)AD=BE，(3)∠DAC=∠EBA，(4)∠ADC=∠BEA再考虑特殊角，(5)显然，∠ABC=二BCA=∠CAB=60?/SPAN>，(6)联系(1)，有∠AGE=∠EBA+∠GAB=∠EAG+
　　
　　∠GAB=∠EAB=60?/SPAN>；进一步推出：(7)∠DGE=120?/SPAN>，(8)D、G、E、C四点共圆，(9)AE·AC=AG·AD，或BG·BE=BD·BC，(10)2AG·AD=BG·BE．(11)∠GDC+∠CEG=180?/SPAN>，(12)△AGE≌△ACD．】
　　
　　三、让手“活”起来——实验、操作的升华
　　
　　传统的平面几何题，注重对学生思维能力的培养，而忽视动于能力的训练．其实，结合题目的特征，把传统几何题改编为实际操作题，让学生的手动一动，不但能提高学习兴趣，而且还能加深学生对题目的理解，强化实践能力．

[1] [2] [3] 下一页