让平面几何题更加生动活泼

　　四、让过程“活”起来——探究过程的升华
　　
　　把几何(数学)的研究过程融入题目中，体现数学活动过程，如猜想、类比、发现，一般化与特殊化，试题由形式单一向形式多样转化，由静态向动态转化．其实，前面的问题也不同程度地体现了探究过程．
　　
　　例10：在一次课题学习活动中，老师提出了如下问题：点P是正方形ABCD内的一点，过点P画直l分别交正方形的两边于点M、N，使点P是线段MN的三等分点，这样的直线l能够画几条?
　　
　　经过思考，甲同学给出了如下画法：如图10，过点P画PE上佃于E，在EB上取点M，使EM=2EA，画直线MP交AD于N，则直线MN就是符合条件的直线．
　　

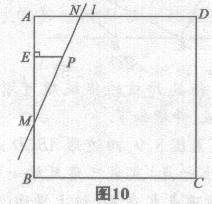
　　根据以上信息，解决下列问题：
　　
　　(1)甲同学的画法是否正确?请说明理由．
　　
　　(2)在图10中，能否再画出符合题目条件的直线?如果能，请直接在图1l中画出．
　　
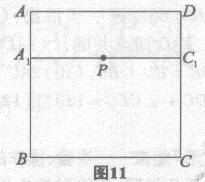
　　(3)如图11，A1、C1分别是正方形ABCD的边AB、CD上的三等分点，且A1C1∥AD．当点P在线段A1C1上时，能否画出符合题目条件的直线?如果能，可以画出几条?
　　

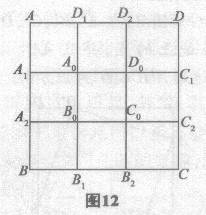
　　(4)如图12，正方形ABCD边界上的A1、A2、B1、B2、C1、C2、D1、D2都是所在边的三等分点．当点P在正方形ABCD内的不同位置时，试讨论，符合题目条件的直线l条数的情况．
　　

　　【点评：例10把以前的静态问题升华为数学过程，是一道关注学生数学活动和探究过程的好题．本题以课题学习的形式来呈现问题，让学生在解决问题的过程中，亲身经历“创设情景——实践探索——建立模型——熟悉模型——反思——应用与拓展”的探究过程．设计新颖，构思精巧，可谓独具匠心!首先，通过判断甲同学解答的正误来创设问题情境；然后让学生在判断正误的互动中，探究出画符合条件直线的理论依据，进而建立“如何画符合条件的直线”的模型(方法)；之后，通过模仿(在画
　　
　　一条符合条件的直线)来熟悉数学模型；接下来，再通过一个特殊位置来反思数学模型，揭示问题本质；
　　
　　最后，把模型放到整个正方形中，实现对模型的应用与拓展．这个题目的布局从一般到特殊再到一般，立足于培养学生发现问题、解决问题的能力和创新意识．由于第(4)小题是前3小题的综合与拓展，所以还需学生有分类讨论的意识．】
　　
　　我们从“应用”“开放”“实践”“过程”对传统题升华为新题型作了概括和探讨，此类升华题已成为近年中考平面几何试题的主流．
　　
　　【作者简介】刘明辉，山西省长治市第19中学．
　　
　　【原文出处】《黑龙江教育》：中学教学案例与研究(哈尔滨)，2010．7／8．40～42

上一页 [1] [2] [3]