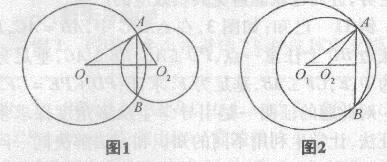
由于平时画相交两到时,都画成两圆心在公共弦两侧的情形,受“习惯”的影响,解题时就片面的只画圆心在公共弦异侧情况(如图1).此时答案为105?/SPAN>,而忽视圆心在公共弦同侧情况(如图2),此时答案为15?/SPAN>.可见,由于“习惯”定势的影响而漏掉一一解,原题中∠O1AO2应该等于105?/SPAN>或15?/SPAN>.
5.类比不当的干扰
学生的学习过程,实质就是在原有的认知结构上探寻新知识的过程,这个过程的关键是怎样由旧知识“类比”迁移到新知识.这种“类比”有时有利于新知识的掌握,但是当新旧知识之间是相交或包含关系时,常会出现类比中的“负迁移”现象,造成解题失误.
例5若a为实数,则-a表示——.
不少学生由于受小学“未知数”表示“正数”的影响,在学习“正、负数”后,又受具体数字,如-1,-4,-1.5等影响,往往认为有“-”号就表示是负数,导致认为“-a”表示负数的错误认识,而-a仍然表示任意实数.
6.思维定势的干扰
在已有知识和经验的基础上,用某种固定的思维方式去思考新问题,会给解题带来一定的消极作用,抑制合理的有效思维而导致解题失误,为此,我们要引导学生克服思维定势造成的障碍,认真分析条件,弄清概念、公式、规律的使用范围,注意相近问题找区别,不同问题找联系,做到快捷、准确地解答.
例6如果关于x的方程(m+1)x2+2x+l=0有实数根,则实数m的取值范围为一——。
受思维定势的影响,很多学生从所给方程的表面形式判断方程是一元二次方程,得m+l≠0且△≥0.即m≠-1,△=4—4(m+1)≥0,故m≤0且m≠-1.方程(m+1)x2+2x+l=0一定足一元二次方程吗?事实上,当m=-l时,方程(m+1)x2+2x+1=0可转化为一元一次方程2x+1=0,该方程也有实根,因此本题的正确答案应是m≤0.
7.约定俗成的干扰
教材巾或教学时有很多“特殊规定”,这些“特殊规定”实际上是编者或教师为了降低教学的难度或者是便于学生学习的一种约定俗成,但是学生在解题时因为受这种约定俗成的影响,生搬硬套,不能灵活运用这些“约定俗成”,从而使解题出现错误的结果.

8.以偏概全的干扰
在解题时片面地运用某个知识点,知识之间不能融会贯通,抓住表面不放,没有去挖掘隐含在背后的本质,往往体现不了不同的思维层次,造成解题失误.

三、“熟题效应”问题的解决
1.学会分析取舍
在练习或考试中,若发现试题中有一些满有把握的“熟题”.在解答时,要学会摆脱“熟题”的束缚,要认真分析题目中已变化的条件,遇到“熟题”时,应先观察题中的条件有没有什么不同,要学会对题目中的已知条件进行取舍,不要盲目下笔求解,要把已知条件和要求的问题弄清楚后再选择最佳方法求解,从而培养思维的深刻性和灵活性,有效防止和克服思维定势的负效应.

于此道题这样分,分类讨论显然是不行的,因为题目中已限定了m≠n,所以在做题时要善于“取舍”,把m=n的情况去掉,就能得到原式的值为-11.
上一页 [1] [2] [3] [4] 下一页
