2.学会思考比较
数学学习的过程实质就是知识的积累储存的过程,随着学习进程不断深入,数学知识也就呈现
面广、类多、量大的情形,优化知识的储存状态,在学习中有利于对知识的回忆、提取、应用、综合等提供有利的“检索途径”,在知识的积累储存时要讲究一博——面广,跨度要大;二专——深刻,见解独到;三精——精简,有概括性;四活——联系,纵横交织.这有利于埘知识结构进行分析和比较,并从分析、比较中找出它们之问的联系与区别,从而增强对“貌合”而“神离”问题的辨析能力,增强思维的灵活性,仿效防止和克服思维定势的负效应.
例10下列各式中一定正确的是()

3.学会寻根求源
数学思维过程就是利用数学知识作“工具”解决问题的过程,解决问题的方法和手段可以多种多样,这就要求我们学会辩证思维,多角度、多方位的思考问题,发挥思维的创造性,灵活运用不同知识解决同一个数学问题,增强思维的变通性,防止思维定势,进而也就能避免其负效应的产生.
例ll已知:如图3,在△ABC中,AB=AC,P是底边BC上任意一点,PD上佃,PE上Ac,垂足分别为D、E,CF⊥AB,垂足为F求证:PD+PE=CF.
对此题的证明一是引导学生从多角度探求多种证法,让学生利用不同的知识和方法解决同一问题,加强学生知识结构的联系,突破思维的“狭隘性”(证法很多,读者可自己完成).二是通过对该问题的引申,探究其结论在不同条件下的应用.


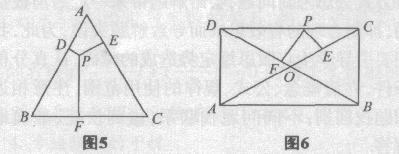
在“矩形”中的应用:如图6,在矩形ABCD中,AB=12,BC:5,JP是DC边上一动点,PE⊥AC于E,PF上BD于F,求PE+PF的长.
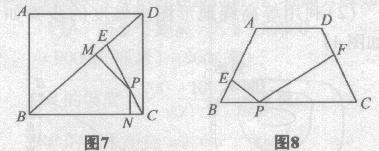
在“正方形”中的应用:如图7,正方形ABCD的边长为a,E是对角线BD上一点,BE=a,P是EC上任意一点,PM上BD于M,PN上BC于N,求PM+PN的长.
在“等腰梯形”中的应用:如图8,在等腰梯形ABCD中,AJD∥BC,∠B=∠C=60?/SPAN>,BC=a,P是BC边上一点,PE上AB于E,PF⊥CD于F,求PE+PF的长.
让学生在“动”与“静”的变化中,抓住问题的本质,引起学生学习数学的兴趣,激发学生思维的创造性,突破思维的“局限性”.
4.学会辩证思维
在教学中,要强化变式训练,不断变换数学知识的呈现形式,使学生在“变”与“不变”中把握知
识的本质属性,逐步由会到熟,由熟到活,真正把握知识的内在联系.
例12(1)解方程x2一3x+2=0;(2)分解因式x2?3x+2;(3)求抛物线y=x2?3x+2与x轴的交点坐标;(4)解不等式x2一3x+2>0.
本大题的四个小题虽然涉及的知识点各异,表达形式不同,但归根结底就是一个解方程的问题,
上一页 [1] [2] [3] [4] 下一页
