初中数学教学环节出声思考的策略

　
　　问：这个垂直和正方形中的直角有什么联系?
　　
　　答：∠ABE=90?/SPAN>，△ABE是直角三角形，BM是高．这里有一个基本图形，∠8=∠9，∠7=∠10．
　　
　　问：目的是关注G是否是DC中点，∠8与∠9已相等(中介问题3)，角的关系要联想对应边的关系．
　　
　　答：考虑△BCG和△ABE的关系．它们是全等的(中介问题2)．刚才没有发现这个基本图形．
　　
　　此题学生出声思考充分体现：通过问答，逐渐明晰思维．在问题解决后，要求学生用出声思考的方式还原整个过程．
　　
　　教师、学生出声思考时要把实际经历的过程如实表现出来，既要暴露成功，同时也要暴露挫折．教师的思维示范要一步一步让学生观察得到，让学生观察到老师在“看到结论，想到要具备它所需要条件”的机理；尤其是要暴露挫折思维，以及碰到挫折时采取怎样的方式思考和处理．
　　
　　(3)答思路及选择该思路的理由．
　　
　　例5点P是□ABCD内任意一点，过P作EF∥AB，交AD、BC于E、F，过点P作GH∥AD交AB、CD于G、H试比较□AGPE与□PFCH的面积大小，并说明理由．
　　
　　出声思考如下：P是□ABCD内任一点，随着P在□ABCD内移动，□AGPE与□PFCH的面积都在不断变化．那么是不是存在点P，使所要比较的两个四边形的面积相等?这个可以肯定．
　　
　　除了一对角线交点，这样的点还有吗?还有的．
　　
　　其实，在对角线BD上的点，都能使两个四边形面积相等，这是什么理由呢?
　　
　　那么自然会想到，在对角线AC上的点呢?
　　
　　进一步想到，除了BD上的点，□ABCD内的其他点呢?
　　

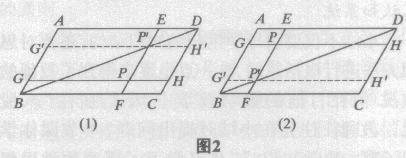
　　操作：如图2(1)、图2(2)，P在△ABD内时，□AGPE的面积小于□PFCH的面积；P在△BCD内时，□AGPE的面积大于□PFCH的面积，这是操作得到的，能证明吗?
　　
　　我想到把GH向下(向上)平移来解决问题．
　　
　　学生出声思考中，反映出他的思维程序——解决什么问题需要什么概念，知道什么规律怎么用，是学生解决问题的方法、策略的显性化过程．
　　
　　三、小组学习。出声思考的主阵地
　　
　　要出声思考，就要有专注的倾听对象、要有有秩序的组织引导和及时反馈评价．在课堂有限的时间内是无法让每个人都有机会面对全班出声思考的，所以小组合作是出声思考最有效的途径．
　　
　　(1)小组内优秀同学的出声思考，对其他同学是一种示范(通过合作评价，学生们一起学习，既要为别人的学习负责，又要为自己的学习负责，让每一个学生都有表现和进步的现实机会)．
　　
　　(2)生生帮扶，实现共同进步．学有困难的学生可以通过小组合作、生生帮扶实现思维指引解决困难；同时，帮扶他人的问学，通过出声思考，让不懂的同学搞懂，自己也会得到长足的进步，需要反复调整出声思考的角度，用不同的出声思考去梳理解决有困难学生的问题，思路要更加清晰，表达要更有条理、更加精炼．要求学生尽可能完善地、有阵对性地给删学提供较多的信息指导，可以使学生将自己零散的知识加以系统化和结构化．
　　
　　(3)生生互为老师，实现普遍出声思考．①互相开系列化问题清单，有利于问题的解决．②轮流当老师．互相教，告诉同学自己是如何做出抉择的，自然地运用出声思考策略．此外，学生之问相互为老师，也有助于学生将自己的思考与其他同学的思考加以对比，从而清楚地了解比自己更好的思维者足如何思学的．③生生过程性评价，较之教师，学生更易站在学生的角度思考问题，更能激发学生表达(表现出声思考)．④有利于对出声思考过程的反思过程的完善，从而促进数学思维能力．
　　
　　学生在一步一步成为理性思考者的过程中，需要教师思维与学生思维的相互交流撞击，通过让学生不断触及、追求逐渐成熟的思维模式达到成人的思维水平．
　　

上一页 [1] [2] [3] [4] 下一页