作者:学夫子
这个是高中逻辑用语里面的内容,相信对于每一个学生都没问题,“p或q”的否定是“非p且非q”,“p且q”的否定是“非p或非q”,今天我们深入一点,挖掘这一结论背后的集合原理。
我们知道,“或”相当于集合里的“并集”,“且”相当于集合里的“交集”,“非”相当于集合里的“补集”,自然有关于逻辑里的一些“法则”,就能用集合的法则解释,就这个“且”与“或”的否定在这里也有着集合的法则。
非(p或q)=(非p)且(非q)
非(p且q)=(非p)或(非q)
对应着集合里的法则就是:
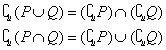
这便是著名的德摩根定理。实际上,逻辑中的这一法则和集合中的这一法则其实是一个定理的不同表现形式而已,而且都是同一个人——即德摩根——发现的。只是由于高中数学没有提到,这里介绍一下,以便大家理解逻辑里面一些结论的本质,而不是简单地停留在记忆层面上。
就好像且的否定是或,或的否定是且,存在的命题是全称,全称的否定是存在,都是的否定是不都是一样,德摩根定理的一个推广就是:“任何一个逻辑运算符,都能找到一个与之对偶的运算符”。这种对偶原理成了电子计算机的核心原理。(来源:学夫子数学博客)
|
