为什么需要弧度制 |
|
|
| 来源:不详 更新时间:2012-12-11 12:19:22 |
|
|
|
|
作者:学夫子
弧度制是一种角度的度量制度,从中学开始讲弧度制开始,就一定有很多学生对弧度制存在的必要性表示疑问——角度制不够吗,为什么还要弄个弧度制?我们听见一些文章里的说法是,因为角度制的数据太大了,使用起来很不方便,而弧度制能够弥补这一点。这当然不是弧度制的真正作用,实际上,采用弧度制唯一的原因就是:它能够让很多公式变得简单。
来看我们的弧长和扇形面积公式:

我们可以看到,弧长与半径和圆心角都成正比,但是这个比例系数太烦了,为了简化公式,我们完全可以重新定义角度的度量制度,使得比例系数为1,而半径r的度量已经确立起来,那么能改变的就只有角度,于是就有了我们的弧度制:
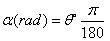
这样定义下的角度能够让弧长和扇形面积公式都变得非常简单,定义本身便给出了角度与弧度之间的互化。所以弧长与半径、角度之间的简单正比关系成为弧度制定义的来源。
这事儿不是欧拉一个人的突发奇想,在物理学中,为了简化公式而定义一个量的度量制度的事情也有过,最著名的莫过于对“力”的度量,牛顿通过实验得到这样一个结论:物体的加速度跟物体所受的合外力F成正比,跟物体的质量成反比,加速度的方向跟合外力的方向相同。即a=kF/m,而在当时并没有关于单位力的度量(或者是另一种度量制度?),于是为了方便,就取k=1,这样一来公式F=ma实际上便成为了力的度量制度来源。
这种通过简单的比值来定义一个新量的方法,在物理学当中得到广泛采用,比如压强,密度等这些概念都是按如此方法定义。当然,弧度制下的角度能够带来数学中的其他好处——一个最著名的就是能使得极限sinx/x趋近于1的速度变得更快。(来源:学夫子数学博客)
|
上一个数学: 数学期末考试应试技巧
下一个数学: 勾股定理的PCK内涵解析 |
|
|
|
|
