勾股定理的PCK内涵解析

动经验：探究图形的基本元素之间的关系、多角度探究几何结构、经历空间推理过程，体验数形结合的思想方法；有助于学生获得更多的数学工具去探索和了解我们生存的空间；有助于发展学生的推理能力，理解证明的意义和过程，体会推理和证明的力量．
　　
　　②勾股定理具有几何和代数的双重特征，是几何与代数的桥梁，勾股定理的证明主要有三种方法——演绎法、变换法(拼图法)和代数法，通过对变换法(拼图法)的学习，有助于学生感受运动和变换．
　　
　　⑧勾股定理的发现、验证及应用的过程蕴涵了丰富的文化价值，通过让学生了解勾股定理的历史、人类对它的研究、它的广泛应用等，有助于激发学生的学习兴趣和自豪感，并体会它的重大意义和文化价值．
　　
　　2．勾股定理与其他数学内容的联系
　　
　　(1)横向联系
　　
　　勾股定理与初高中的其他数学内容有着广泛的联系，如初中的无理数、方程、三角函数、四边形、圆和变换，高中的立体几何和平面解析几何．
　　
　　(2)纵向联系
　　
　　小学阶段，学生已经了解了三角形三边之间的关系：两边之和大于第三边．
　　
　　初中阶段，在学习勾股定理之前，学生探索并掌握了直角三角形的性质：斜边上的中线等于斜边的一半，30?/SPAN>角所对直角边是斜边的一半．
　　
　　而勾股定理从边的角度进一步定量刻画了直角三角形的特征，加深了学生对直角三角形的认识和理解．
　　
　　高中阶段，学生继续学习任意三角形中边长与角度之问的数量关系，需要掌握正弦定理和余弦定理，而勾股定理就是余弦定理的一种特殊情况．
　　
　　从上述学习链条我们可以发现，学生对于三角形边角关系的学习，经历了从定性到定量，一般到特殊再到一般的过程．
　　
　　3．学生在学习勾股定理时可能出现的困难
　　
　　虽然勾股定理的证明方法据说超过400种，但是让学生能够在思路上比较“自然地”想到证明方法是困难的，而且，从让学生体验知识发现过程的角度讲，要想让学生“再发现”勾股定理更是难上加难．
　　
　　对北京市市级骨干教师的问卷调查结果也表明，70.6％的老师认为勾股定理的证明思路难以想到．
　　
　　通过教学设计文本分析进一步可以发现在勾股定理第一课时的学习过程中，学生可能出现的困难主要是勾股定理的发现和证明思路的获得．
　　
　　4．帮助学生学会勾股定理的教学策略
　　
　　通过课例分析发现，目前探究勾股定理常用的教学方法有两种，一种是让学生测量直角三角形三条边的长，让学生猜想三条边长之间的数量关系，但采用这种方式，学生是不容易猜想出三边之间的平方关系的，一是测量本身有误差，二是学生很难想到平方关系．
　　
　　第二种探索勾股定理的方法是利用如下方格纸(图2、图3)进行探究．
　　

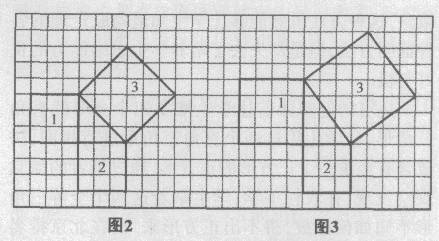
　　首先让学生计算直角三角形三边的平方分别是多少，只要能计算出三边的平方，直角三角形三边之间的平方关系就很容易猜想出来．而直角三角形边长的平方实际上就是每边上的正方形的面积．其中正方形l和正方形2的面积可以通过数方格的方法直接数出来，而斜边上正方形(正方形3)面积的计算则有一定的困难．
　　
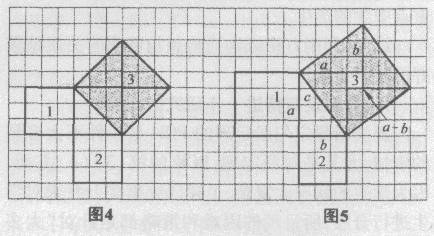
　　常用的方法有“割”，如图4、图5所示．
　　

　　另一种常用的方法是“补”，如图6、图7所示．
　　

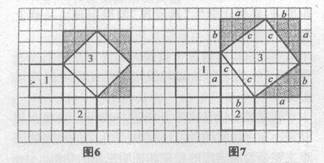
　　上述在方格纸上运用内割法或外补法求斜边上正方形面积的活动蕴含了勾股定理的证明思路，由图5可得：c²=(a－b)^{上一页 [1] [2] [3] [4] 下一页}