勾股定理的PCK内涵解析

2+4(1/2 ab)，由图7可得：(a+b)²=c²+4(1/2 ab)，化简之后就得到a²+b²=c²．因此，利用方格纸探究可以帮助学生较顺利地猜想出直角三角形三边的关系，同时水到渠成地获得定理的证明，使勾股定理的学习一气呵成．
　　
　　证明勾股定理有的老师采取的是直接告诉的策略，这种方法虽然能够让学生知道勾股定理的各种证明方法，但是却失去了培养学生思维能力的良好契机．
　　
　　还有的老师课前让学生准备四个全等的直角三角形，让学生用这四个直角三角形进行拼图，拼成含有至少一个正方形的正方形．通过笔者的课堂观察发现，在农村中学，学生拿着这四个全等三角形不知如何摆放，拼不出正方形来．而在北京排名靠前的重点中学的重点班，学生则能够比较顺利地拼出如下(图8、图9)两个正方形．
　　

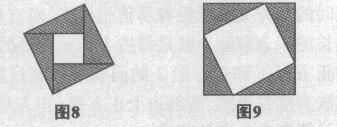
　　由此可见，采用让学生动手操作的策略(拼图)启发学生获得证明勾股定理的思路比较适合重点中学的学生．
　　
　　综上，利用方格纸沟通猜想与证明的关系是较好的教学策略．
　　
　　六、思考及有待进一步研究的问题
　　
　　要清晰界定勾股定理的PCK是一件不太容易的事情，尤其是勾股定理：PCK的第(3)(4)方面，因为学生的状况太复杂．上述研究事实上并未对学生进行分层，所呈现的困难和策略都是针对“大多数”学生而言的，另外，即使是同一种教学策略，在真实的课堂教学中，教师的具体处理也是不同的，效果自然也不一样．
　　
　　另外，笔者一直有一个困惑，教师采用何种教学策略是否一定受他PCK前两方面知识的影响?比如说，教师让学生探索勾股定理的证明方法而不是采取直接告知的教学策略，是因为该教师知道勾股定理对于学生的思维价值，还是新课程倡导探究的学习方式?再比如说，教师采用方格纸的策略帮助学生探索勾股定理，是因为该教师自己清楚勾股定理中包含的面积关系、方格纸能够沟通猜想和证明之间的关系，还是教材当中提供了方格纸这样一种方法?事实上，笔者曾经在所任教的两个数学教师培训班问过同样一个问题，那就是你如何看待教材中所提供的用方格纸探究勾股定理这样一种方法?老师们的回答基本上都是：因为利用方格纸学生能很容易地猜想出勾股定理．从老师们的回答来看，他们并没有意识到这种方法事实上还很自然地给学生提供了证明勾股定理的思路，因此在汪明勾股定理的教学环节，又另辟蹊径：如间接向学生介绍勾股定理的多种证明方法，或采取前述拼图的方法等等，因而使勾股定理的教学没有达到应有的目的，错失了培养学生各种能力的机会．
　　
　　数学教师关于勾股定理这个特定课题的PcK怎样?教师采用何种教学策略是否一定受他PCK前两方面知识的影响?这都是有待进一步研究的问题．
　　
　　参考文献：
　　
　　[1]Shulman，Ls．1'hoseWholunderstand：Knowledg~GrowthinTeaching[J]．EducationalReseaI℃h，1986，15(2)：9．
　　
　　[2]GrossmarL，PL．TheMa．king(订a1'eacher：‘FeacherKno,ⅣledgeandTeacherEducatioll[M]．NewYork：TeachersCoilegePress，1990：7～9．
　　
　　[3]张顺燕．数学的源与流[M]．北京：高等教育出版社，2000．
　　
　　[4]朱哲．中美两国数学教科书中的”勾股定理”比较——以北师大版《数学》和美国《发现几何》为例[J]．数学通报，2009，(2)．

上一页 [1] [2] [3] [4]