向量基本定理和广义坐标系

作者：学夫子
　　
　　从一个角度来说，向量基本定理是初等数学通往高等数学的桥梁(抽象代数)，如果抽出“平面空间”这一实在的事物，并且将维度扩展，就得到我们抽象代数里的核心概念——线性空间。我们在中学里只学过平面向量基本定理，实际上还有空间向量基本定理。
　　
　　平面向量基本定理：考虑平面里的两个非共线向量e和f，则这个平面里的任何向量a都可以用e和f来表示，即存在数对(m，n)使得：a=me+nf。
　　
　　空间向量基本定理：考虑空间里的三个不共面非零向量e、f和g，则空间里的任意一个向量a都可以用e、f和g表示，即存在一个数对(m,n,l)使得a=me+nf+lg.
　　
　　这个定理是线性空间理论的基础定理，由他就可以建立起“坐标”的概念，对的呢没有听错，就是坐标。我们在中学里接触过最多的坐标，就是我们的直角坐标系，不过这只是坐标系家族里特殊的一种而已，实际上真正坐标的概念是下面的：我们以平面坐标为例考虑平面里任意两个非共线向量e和f，e和f就可以称作此平面里的坐标系(更恰当的说法是基底)，若对该平面里的任意一个向量a，a=me+nf，则称(m,n)为向量a在该坐标系下的坐标。
　　
　　如上图类似于直角坐标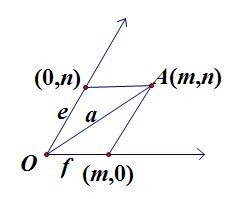

系，e和f分别是该坐标轴上的单位向量，对于A点，做两条坐标轴的平行线，与坐标轴的交点位置就分别是A点的e和f坐标。而对于我们的直角坐标系，其实就是两个互相垂直的单位向量作为基底而已。
　　
　　在这样一个坐标系下，很多平面直角坐标下的性质都不变，不过涉及到直角的就要变化，比如两点间的距离公式等。不过有一点我们在这里得要注意一下，那就是直线方程在任何坐标系下其方程形式保持不变，都可以写成y=kx+b的形式，这点也许就是“线性”的魅力吧！我们可以看出来
　　

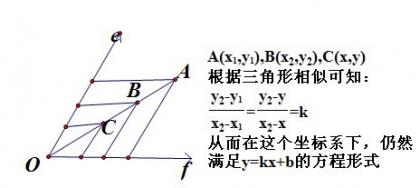
　　我们同理可以导出这样空间坐标系的概念，以及“平面方程”在空间的任意坐标系里的方程都满足ax+by+cz+d=0的形式。
　　
　　这个结论是很重要的。这篇文章是明天文章的准备，明天的内容才是精彩的内容，本来有些麻烦，但若是了解了我们的今天的内容，那么将变得异常的简单。（来源：学夫子数学博客）
　　