初中数学教材分析之从宏观到微观

　　
　　2．析出核心内容、内容核心以及所蕴涵的数学思想方法
　　
　　分析教材不仅要理清教材内容的逻辑结构，更要析出对数学学科具有重要影响且处于主干地位、对学生数学认知结构具有不可或缺的基础作用的核心内容以及核心内容的内容核心，还要析出内容本身所蕴涵的数学思想方法．本节内容的核心内容是“函数的概念”，函数概念的核心是“单值对应关系”，“变量、常量”蕴涵分类思想，“函数”蕴涵变化思想和对应思想．
　　
　　3．领会正文、例题、习题的编写意图
　　
　　此过程主要研究教材内容究竟是如何围绕核心内容展开的，怎样突出内容的核心的，如何渗透数学思想方法的．
　　
　　本节内容教材呈现的正文主要包括两部分：第一部分通过5个例子(①匀速运动中路程和时间的关系；②电影院中票房收入和电影票张数之间的关系；③弹簧受力后长度和所挂重物之间的对应关系；④圆半径和面积之间的关系；⑤在周长一定的前提下，长方形面积．s与长的对应关系)抽象概括出变量和常量的概念，为引出函数概念作铺垫，同时，在抽象变量、常量概念的过程中渗透分类思想；第二部分具体分析5个例子中的两个变量间的对应关系，并思考用图象和表格表示的两个变量间的对应关系，进而概括出函数的概念，体现变化思想和对应思想．正文第一部分的5个例子，从内容上看，都有变量和常量，而且都含有两个变量；从背景上看，有数学问题也有物理问题，有代数问题也有几何问题，有学生实际生活中的常见问题也有纯数学问题，这些问题背景都是学生熟悉的、贴近学生数学现实和生活现实的素材；从呈现方式上看，有的需要填表，有的需要求值，所有的都需要写关系式；从结果上看，关系式中有的用变量的一次式表示，有的用二次式表示，有的用二次根式表示，并且自变量的范围有的为有限的正整数，有的为开区间；从反映的本质上看，5个例子的共同特征凸显了变量和常量概念的本质属性，为函数概念的引入作了很好的铺垫；从数学思想方法上看，5个例子的本质特征蕴涵着分类思想．在概括出变量、常量的概念后，教材中的“思考”和“练习”(“思考”：具体指出上面的各问题中，哪些是变量，哪些是常量．“练习”：举出一些变化的实例，指出其中的常量和变量)又从两个不同的侧面对变量和常量进行再认识，提高学生对变量、常量概念本质的理解和对
　　
　　分类思想的感悟．第二部分，教材对5个例子一一进行细致分析，主要解释以下几个方面的意义：(1)在一个“变化”过程中；(2)存在“两个”变量；(3)这两个变量具有一定的“联系”；(4)这种“联系”使一个变量的变化引起另一个变量也“随之”变化；(5)这个变化之间存在“单值对应”关系．整个分析过程紧紧围绕本节核心内容(即函数)的内容核心(即单值对应关系)，突出了关键字“每”和“唯一确定”的意义，即“每”——任意、穷尽所有，“唯一确定”——存在但没有第二个，同时渗透变化思想和对应思想．在第二部分，教材又以心电图和中国人口统计表为背景呈现了用图象和表格表示的函数关系，为凸显函数概念的本质特征提供丰富的素材，同时也为进一步研究函数的不同表达方式作铺垫．教材在概括出函数概念并定义了自变量、函数、函数值后，又对前面的例子进行再认识，并用新的表达方式解释两个变量之间的关系，以加深学生对函数概念的理解，提高学生的表达能力．教材中的练习是分别以几何问题和具有生活背景的代数问题为载体的两个函数，要求指出其自变量、函数，并写出解析式．此题的作用是对本课时的核心内容的强化，可以提高学生对函数概念核心的理解和对变化思想、对应思想的感悟．
　　
　　本节内容教材没有例题，涉及的相关习题主要有4道．第l、2题分别以代数、几何内容为背景，指出题中常量与变量，自变量与函数，并写出解析式，第2题还要求写出自变量的取值范围．这两道题具有针对性和层次性，习题紧紧围绕本节的核心内容进行巩固练习．第3题是判断题，判断y=3x－5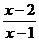，y=

，y=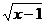

是否为函数，并说明理由，再举出一些函数的例子．第4题(教材中的第6题，前三道题分别为教材的第1、2、3题)是判断所给的4条曲线是否表示函数．这两道题通过以解析式、图象两种不同方式呈现变量间关系，让学生判断两个变量是否为函数关

上一页 [1] [2] [3] 下一页