作者:学夫子
搞了好几篇证明根号2为无理数的文章,包括《无限递推法证明根号2为无理数》,《再次证明根号2为无理数》等。我们当然不能停留在根号2这个层次上,今天的任务就是要来证明,对于任意一个开不尽方的d,根号d都是无理数。这第一个首要的问题,就是如何说明“d开不尽方”这句话?简单的数论给我们提供答案:
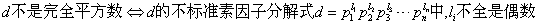
这个是重点,应该还是好理解吧.并且这个不是偶数的li是重点中的重点.我们不妨设l1为奇数,下面我们要证明,若√d=m/n,则m必定能被p1整除,n也能被p1整除,从而导出矛盾.就像我们在证明√2=m/n不成立的时候证明m和n都能被2整除一样.
证明:若存在互质的m和n使得√d=m/n,既有m2=dn2,将d进行素因子分解得到:
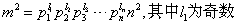
很显然的,m2必须能被p1整除,从而m也必然能被p1整除.下面我们来证明n也能被p1整除.
既然m能被p1整除,那就设m=k(p1)γ,其中k已经不能被p1整除,换句话说,p1已经被提干净了.则:
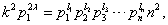
显然必须要2γ≥l1,这个应该好理解吧.一个数a要能够被b整除,则a中的素数分解中,任何一个素数的次数必须比b的大,比如54能被9整除,那么54中3的次数一定要比9大才行.然而l1为奇数,所以2γ≥l1实际上就是2γ>l1,这一步是关键的一步,他告诉我们,等式左边的p1一定比右边的多.将等式化成:
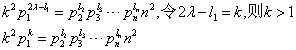
这样一来,n2就必然能被p1整除,故n也必被p1整除.这样一来,m和n都被p1整除,与他们互质矛盾,从而证明√d是一个无理数.(来源:学夫子数学博客)
|
