勾股定理，圆幂定理和平方差公式

　　作者：学夫子
　　我们都知道勾股定理，圆幂定理和平方差公式，如果有一个式子能把他们连起来的话你是不是会感觉很爽？其实圆幂定理已经可以将这三个公式联系起来，让我们看看平方差公式的一个奇妙运用。不管怎么说，对于提高数学兴趣还是很有好处的。

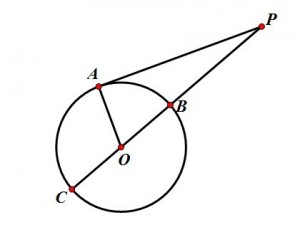
　　如图所示的几何关系，PA为圆0切线，PC过圆心交圆于B、C两点，那么我们根据圆幂定理就有下面的式子成立：
　　PA²=PB×PC
　　很普通的一个结论，我们现在令PO=x，AO=y，则根据勾股定理可以知道：PA²=y²-x²，另一方面，PB=y-x，PC=y+x，带入圆幂定理的式子里又有：
　　PA²=(y-x)(y+x)，所以又：
　　y²-x²=(y-x)(y+x)
　　而这正是我们的平方差公式，这是显然成立的。可见很多公式本质上都是一样的，善于发现就能够将他们联系起来。而且据我看，我们还可以直接利用它来证明勾股定理！因为PA²=PB×PC只需要用到△PAB∽△PCA，这一点只需要用到OA垂直于PA以及一些角度关系，相似原理自然也和勾股定理无关，这样我们就可以证明勾股定理了：
　　PA²=(y-x)(y+x)=y²-x²
　　勾股定理就这样证明，这里面应该没有涉及到循环论证的吧，这两天老犯错，如果有错，还请指点。（来源：学夫子数学博客）