作者：学夫子
对于目前来说，差比型数列的求和算是数列这一章较难的内容了。其求和多采用的是错位相减法，该法有它非常好的优点——那就是方法直接。对于不习惯数学中拐弯抹角的同学来说非常适合，很多学生反映此法计算量较大，其实若细细掌握其中要领，完全可以避免这一类错误，速度也能得到提升。笔者在平时的学习中捉摸出了另外的几种方法，各有千秋，放在这里共勉。在这里就不再介绍错位相减法，如有同学对此法有不理解或容易犯错之处，可在下方留言，我定会细细解答。
一：裂项求和法
在未搬家之前，我曾经写过此法的文章。下面就以最简洁的方式描述。
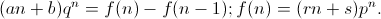
（r，s为待定常数）。注意f(n)在形式上和an一样，都是一次函数与指数函数的乘积，且指数函数部分与原来一样。接下来，你可以采用特殊值法或是待定系数法求r和s。
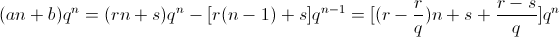
对应系数相等即可求出r和s，进而通过裂项求和法求解，且此法还不用讨论n=1的情况。
二：错位相减法的另一版本
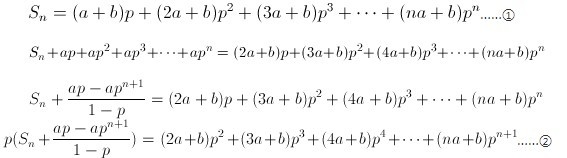
①-②既得Sn的解，因为中间的全都消掉了。这种方法本质上仍然是错位相减法。只是因为错位相减法本身相减的时候无法把中间消掉，留下一个等比数列求和，而此法是先把该等比数列减掉，以便中间能够直接去掉。
三：导数法
此法是建立在如下一个认识上：任何一个差比型数列求和最终都可以归结为具有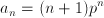
的前n项和。这里故意留成n+1而不是n，就是为了导数的应用做准备。且将an看成关于p的幂函数，而不是关于n的指数函数。那么
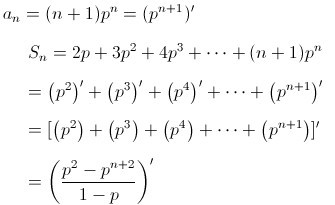
利用函数除法求导公式即可求解。求解完以后需要将本身的p值带回去。在实际应用中，p往往是个常数，次数需先将其看成未知数，最后再带回。（来源：学夫子数学博客）
