无法直接求通项？就找递推吧！

根据递推求通项那绝对是数列考试的重点对象，这个运气好点的，考官会把递推关系给你，多数情况下你只需要按部就班去做就行。这个运气不好，递推关系还得你自己去找。其实找这关系倒是好找，关键就在于很多同学不知道去找。总之一句话：当我们无法通过常规思路求通项时，你就找递推吧！

【例1】设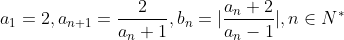 $a_{1}=2,a_{n+1}=\frac{2}{a_{n}+1},b_{n}=|\frac{a_{n}+2}{a_{n}-1}|,n\in N^{*}$ ，则数列 $\left \{ b_{n} \right \}$ 的通项公式 $b_{n}=$ __________。

点拨：很显然本题并不是让你求出a_n然后然后再代入，若是如此，此题便真的没什么意思了。而且我们直接求a_n也并非易事，已经超出中学的能力范围。我们需要找到数列b_n的递推。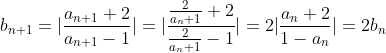 $b_{n+1}=|\frac{a_{n+1}+2}{a_{n+1}-1}|=|\frac{\frac{2}{a_{n}+1}+2}{\frac{2}{a_{n}+1}-1}|=2|\frac{a_{n}+2}{1-a_{n}}|=2b_{n}$ 。这是个等比数列，接下来的事情……

【例2】已知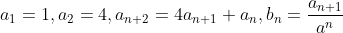 $a_{1}=1,a_{2}=4,a_{n+2}=4a_{n+1}+a_{n},b_{n}=\frac{a_{n+1}}{a^{n}}$ ,求b_n。

点拨：遇到这一类题目，条件给的是一个数列的递推，而让你求得是另一个变形数列的通项，十之八九就是让你寻找变形数列的递推。就算有时候给出的数列递推是能够求该数列通项的，但是只要题目中涉及到一个变形数列

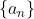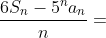【例3】数列 $\left \{ a_{n} \right \}$ 中， $a_{1}=1,a_{n}+a_{n+1}=(\frac{1}{5})^{n}(n\in N^{*}),S_{n}=a_{1}+5a_{2}+5^{2}a^{3}+\cdots +5^{n-1}a_{n}$ ，则 $\frac{6S_{n}-5^{n}a_{n}}{n}=$ _________.

点拨：此题若按照传统的求出a_n和S_n，当然也是可以的，但这显然不是此题的考察目的，最后让你做一个简单的组合实在是太狗血。我们要找的，仍然是递推。

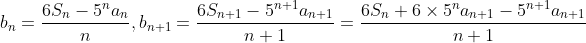
$b_{n}=\frac{6S_{n}-5^{n}a_{n}}{n},b_{n+1}=\frac{6S_{n+1}-5^{n+1}a_{n+1}}{n+1}=\frac{6S_{n}+6\times 5^{n}a_{n+1}-5^{n+1}a_{n+1}}{n+1}$

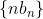$=\frac{6S_{n}+5^{n}a_{n+1}}{n+1}=\frac{6S_{n}+5^{n}\times [(\frac{1}{5})^{n}-a_{n}]}{n+1}=\frac{6S_{n}-5^{n}a_{n}+1}{n+1}=\frac{nb_{n}+1}{n+1}$ $\Rightarrow (n+1)b_{n+1}-nb_{n}=1$ ，即数列 $\left \{ nb_{n} \right \}$ 为等差数列。再来求通项就简单多了。

【例4】设 $f_{1}(x)=\frac{2}{x+1},f_{n-1}(x)=f_{1}(f_{n}(x)),a_{n}=\frac{f_{n}(0)-1}{f_{n}(0)+2},n\in N^{*},$ ，求a_n。

点拨：很多学生不是被这道题难住的，而是被题目这一啪啦架势给吓住的，我们不能直接求a_n，那就找递推。

$a_{n-1}=\frac{f_{n-1}(0)-1}{f_{n-1}(0)+2}=\frac{f_{1}(f_{n}(0))-1}{f_{1}(f_{n}(0))+2}=\frac{\frac{2}{f_{n}(0)+1}-1}{\frac{2}{f_{n}(0)+1}+2}=\frac{1-f_{n}(0)}{2f_{n}(0)+4}=-\frac{1}{2}a_{n}$ ，所以a_n是一个等比数列。

不仅是这种文字类的题目，往往一些看图找规律类的题目也可以这样来。还是那句话，找不到通项，就找递推吧！