圆锥曲线光学性质题一个

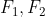【原题】设为椭圆 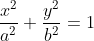的两个焦点，P为椭圆上任一点，延长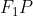至E，使|PE|=|PF2|，l为EF2的垂直平分线，求证，l与椭圆只有唯一的公共点。

证明：本题考查圆锥曲线的光学性质——椭圆上一点P处的切线，与两焦半径之间的夹角相等，反过来也成立。

在本题中，很容易知道，∠EPA=∠APF2=∠BPF1，从而知道l为该椭圆的切线，自然就只有一个交点（当然是针对于椭圆而言，其他曲线可不一定），该交点就为P。

本题来自《更高更妙的数学思想》一书，原书采用的是反证法，即假设直线与椭圆有两个交点，然后推出矛盾。现在看来也是用不着的，简单应用一下光学性质即可。