【原题】已知函数=x^{3}+ax^{2}+bx+c) ,下列结论中错误的是( )
,下列结论中错误的是( )
A.=0)
B.函数) 的图像是中心对称图形
的图像是中心对称图形
C.若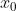 是函数
是函数) 的极小值点,则
的极小值点,则) 在区间
在区间) 上单调递减
上单调递减
D.若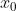 是函数
是函数) 的极值点,则
的极值点,则=0)
此题乃2013年新课标2试题,选择题第11题,这个位置的题目该是有一定难度的吧。不过这道题就是A、B两个吓人而已,重点是第三个,很容易判定选项C是错的,你只需要知道“极小值点”的定义即可。D选项的正确性不容置疑,那么也就是说A、B两选项是对的,这就有话要说了。
选项A的意思其实就是说,三次方程一定有实数解,实际上不止如此,我们甚至可以断定,奇数次方程也一定有实根,还得听我到来:
若一个多项式方程没有实根,那么就一定有虚数根,还知道复数里面有个叫“共轭复数”的概念吧,共轭这个词真的很好,唇亡齿寒,一起出生入死,这个定理便是这种感情的描述:如果a+bi是多项式方程的根,那么其共轭复数a-bi也是该方程的根。该定理的核心是:^{n}=\overline{Z^{n}}) 其中
其中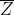 代表Z的共轭复数,比如
代表Z的共轭复数,比如^{2}=\overline{(a-bi)^{2}}=\overline{a^{2}+b^{2}-2abi}=a^{2}+b^{2}+2abi) 。由此便可以很容易证明:
。由此便可以很容易证明:=\overline{f(Z)}) ,所以若f(Z)=0,那么
,所以若f(Z)=0,那么) 也肯定为零。
也肯定为零。
这个定理是在说,多项式方程的根都是成双成对出现的,也就是虚根的个数是偶数个,而奇数次方程的复数根是有奇数个的,自然就肯定有一个实数根。由此我们可以断定,五次、七次这些方程肯定有解,只是我们无法求得而已,这就叫可望不可即。
第二个更有意思了,三次函数一定是一个中心对称图形,我们不打算证明,且看看这一结论的用处,因为我们可以根据这一结论去追寻卡尔达诺求解三次方程的思想哟。
若函数=x^{3}+ax^{2}+bx+c) 的图像是一个中心对称图形,这就意味着,我们可以通过左右平移(也就是只改变自变量x),使得对称点在Y轴上。对称点在Y轴上就意味着,只需要上下平移就可以使之移动到原点而变成奇函数,这就意味着,对称点在Y轴上的话,函数f(x)的形式就是一个奇函数+常数。我们假设左右平移的量为m,那么有:
的图像是一个中心对称图形,这就意味着,我们可以通过左右平移(也就是只改变自变量x),使得对称点在Y轴上。对称点在Y轴上就意味着,只需要上下平移就可以使之移动到原点而变成奇函数,这就意味着,对称点在Y轴上的话,函数f(x)的形式就是一个奇函数+常数。我们假设左右平移的量为m,那么有:
=(x-m)^{3}+a(x-m)^{2}+b(x-m)+c)

x^{2}+(3m^{2}-2am+b)x+m^{3}+am^{2}-bm+c)
所以只需要让a-3m=0即 即可,此时
即可,此时=x^{3}+(b-\frac{a^{2}}{3})x+\frac{4a^{3}}{27}-\frac{ab}{3}+c) 。这一推导过程其实也间接证明了f(x)关于中心对称的正确性,顺便还得出了其对称中心为
。这一推导过程其实也间接证明了f(x)关于中心对称的正确性,顺便还得出了其对称中心为)) ,这便是300多年前卡尔达诺所采用的方法。
,这便是300多年前卡尔达诺所采用的方法。
一道高考题,背后所涉及的东西可不少。
来源:学夫子博客
