今天又是分享一道有着高等数学背景的高考题,这是来自福建2013年文科数学的一道填空题,其背后涉及到康托尔的理论。
【原题】设是的两个非空子集,如果存在一个从到的函数满足;
(i),x\epsilon&space;S&space;\right&space;\}) ;(ii)对任意的
;(ii)对任意的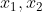 ,当
,当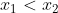 时,恒有
时,恒有<f(x_{2})) .那么称这两个集合“保序同构”.现给出以下3对集合:
.那么称这两个集合“保序同构”.现给出以下3对集合:
①;A=N,B=N+
②;A={x|-1≤x≤3},B={x|-8≤x≤10}
③:A={x|0<x<1},B=R
其中,“保序同构”的集合对的序号是____________(写出所有“保序同构”的集合对的序号)
解析:稍加分析即可知道,本题实际上就是要寻找“定义域为A,值域为B的单调递增函数”,对于第一对集合,y=x+1(x∈N)恰好满足;第二对集合,![y=\frac{9}{2}x-\frac{7}{2};(x\epsilon [-1,3])](http://latex.codecogs.com/gif.latex?y=\frac{9}{2}x-\frac{7}{2};(x\epsilon&space;[-1,3])) 便很符合,实际上对于任意两个闭区间或开区间,都可以构造这样的函数;至于第三对集合,有些难度,一个比较容易想到的函数是
便很符合,实际上对于任意两个闭区间或开区间,都可以构造这样的函数;至于第三对集合,有些难度,一个比较容易想到的函数是
;(x\epsilon&space;(0,1))) ,其图像如右图所示,实际上,对于任意一个开区间(a,b),都可以构造一个值域x∈R的函数。由此可以知道,题目所给的任何一对集合都满足保序同构。
,其图像如右图所示,实际上,对于任意一个开区间(a,b),都可以构造一个值域x∈R的函数。由此可以知道,题目所给的任何一对集合都满足保序同构。
回味此题,特别是最后一个我们可以发现:既然可以构造一个定义域为(0,1),值域为R的单调递增函数,这就意味着可以建立一个从(0,1)到R的一一映射,这就意味着“(0,1)内的实数与R内的实数个数是相同的”,这便是康托尔当年所发现的“基数”——只要能建立起一一对应的集合,就说这两个集合的基数相同。对于一般的,有下面些结论成立:
①[a,b],(a,b],(a,b)等实数区间于R基数相同;
②N,Q,Z,N+的基数相同
但是N与R,(a,b)等的基数就不相同,你可以形象化地理解为一个离散,而一个连续,对于应付往后的类似高考题已经足够。
来源:学夫子博客
