以下内容的前提，是你得首先清楚三角函数值得符号问题，你只需要记住sinx符号由纵坐标决定，而cosx符号由横坐标决定即可。1：轴上角的函数值
什么叫轴上角？终边在坐标轴上的角即为轴上角，从角度来说，只要是90°或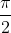
的整数倍，该角度就一定是轴上角。
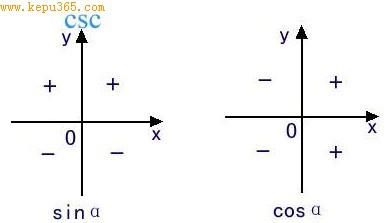
记住下面一句话：“正正相交为1，负负相交为-1，正负相交为0”，什么意思呢？如上图所示，我们要计算sin180°，而180°的终边是二四象限的交线，根据“正负相交为零”，立马可以得到sin180°=0；又如要计算cos（-180°），找到-180°的终边，位于x轴负半轴，是二三象限的交线，根据“负负相交等于-1”，立马可以断定cos（-180°）=-1.细细品味，其中还有零点判定定理的味道在里面呢！
当然这个方法只适合于sinx和cosx函数，对于tanx，则更简单：Y轴上无意义，X轴上全为零。
注：该观点转载自微课网。
3：非轴上角的函数值
许多老师对于这种问题的方法都是：先减整圈，再减半圈，最后减去锐角。其实用不着这么麻烦，你只需要知道三角函数的符号，外加那么几个特殊角函数值（30°，45°，60°），至于0°和90°，其实都已经拿到我们的轴上角范畴去了，几年了记这三个该没什么问题吧！那么计算特殊角函数值就化为三大步：找终边；算出终边与x轴夹角；算出夹角的相应函数值，加上函数值符号。这其中，若所给角度大于360度，先减去整数个360°，目的是为了我们找终边的时候方便些。
例：计算cos960°。
解：cos960°=cos240°（减去2×360°），画出240°的终边，容易算出与x轴夹角为60°，sin60°=
，又根据240°终边所在象限知，cos240°该为负值，所以cos960°=-。
来源：学夫子博客
