把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比。其比值是一个无理数,取其前六位数字的近似值是0.618034。由于按此比例设计的造型十分美丽,因此称为黄金分割,也称为中外比。这是一个十分有趣的数字,我们以0.618来近似,通过简单的计算就可以发现:
1/0.618=1.618
(1-0.618)/0.618=0.618
这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域,而且在管理、工程设计等方面也有着不可忽视的作用。
让我们看一个运筹学方面的例子。假设有一个原料配方设计任务,已知某种添加剂的使用量只有一个最佳值,为了清楚,我们用图来表示,横坐标代表添加剂用量,纵坐标是效果,假设实际情况如红色曲线所示。如何通过试验尽快找到这个数值呢?若以克为最小计量单位,我们绝不能从1克开始,每次增加1克,一次一次地做试验,因为一般说来这样做的效率太低。
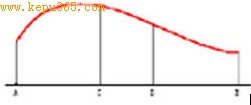
利用黄金分割比可以设计这样的算法:首先确定一个添加剂使用量的搜索范围,在这个范围内仅有一个值是最好的,例如选取1克和100克为搜索范围(对应于图中的A和B)。然后在此区间内再选两个试验用量,这两个试验量是C=(1-0.618)х(B-A)=0.382х(B-A)和D=0.618х(B-A)。
由于以克为最小计量单位,所以C和D都要取整数,C和D两个量进行试验的结果可能有三种情况:甲、C比D好,乙、D比C好,丙、C、D一样好。对于这三种情况,我们分别讨论如下:
甲情况:由于C比D好,所以可以断定最好值不应比D还大。也就是说下一步只需在A到D的范围内寻找就可以了,这意味着第二次的搜索范围大约是第一次的0.618。若以A和D为新一轮搜索的A和B,则上一阶段搜索的试验点C根据前述的关系可知,恰好位于新区间的0.618的位置,即相当于新搜索区间的D。我们只需按上面的公式再求一个新的试验点C,就可以重复上述过程了。
乙情况:和甲情况相反,舍弃比C小的部分,新一轮的搜索范围为从C到B,其长度仍是第一次的0.618。以C和B为新一轮搜索区间的A和B,由于上一次的试验点D正好位于1-0.618=0.382的位置,所以是新一轮的试验点C。我们只需按上述公式再求一个新的试验点D,就可以重复上述过程。对于甲、乙两种情况,新一轮的搜索都只需做一次试验即可。
丙情况:由于C、D一样好,所以可以断定最好值在C和D之间,即下一步的搜索区间是从C到D,此时的搜索区间只有上一次的0.236。此时可将原来的C和D看作新的A和B,再按前法求出新的C和D即可重复前面的过程了。
如此重复寻找,直到新的搜索区间小于或等于1时,就可以结束了。
这个算法的好处是能按至少0.618的速度缩小搜索区间,而且一般情况下前一次的试验结果对于下一次是有用的。因而可能使用最少的试验次数尽快找到最佳结果。这样的方法常常用于最优化设计,特别是当待确定的参数只有一个的情况。黄金分割比的用途早已超出了艺术范畴,这也是时至今日仍然有许多人还在热心于他的研究的原因。
