我们说,思维能力是数学能力的核心。著名美籍华裔科学家、诺贝尔奖获得者杨振宁教授说:“优秀的学生并不在于优秀的成绩,而在于优秀的思维方式。”而创新思维可以说是优秀思维方式的精品。诺贝尔奖新得主朱棣文教授新近说到“创新精神最重要”。
这篇短文,我们将从不同侧面、不同角度给出若干具有新意的题目。解决这些题目需要灵活运用学过的相关知识,还要会有机地迁移知识或做好转换工作。整个解题过程也检测着你的创新精神与创新思维。
【题目】计算1998+1997-1996-1995+1994+1993-1992-1991+…+6+5-4-3+2+1
这道题,要是按部就班自左向右依次计算,也可以算出结果。但运算量太大,也过分繁琐。稍有闪失,还可能全题出错。因此,这种笨拙的解法不可取。
肯动脑筋的同学,经过审题会发现:①题目中的“加数”或“减数”自左至右,依次少1;②题目自1998向后,都是先两个数相加,再连减去两个数。因此这样想:从1998起,由左向右,每四个数组成一组[例如(1998+1997-1996-1995)],而每组数中,第一个比第三个大2,第二个比第四个大2。正因如此,所以这样的每一组数的计算结果都相同,都等于4。
这样一来,问题的关键就转化为:原式总共可分成多少个这样的组?是否有剩余(即到最后不足一组)?
因为题目中涉及加减运算的数一共有1998个,每四个一组,共有1998÷4=49(组)…2(个),即总共可分成499组,还剩两个数。而且前面已分析:这499组数的计算结果全等于4,所以有:
原式=(1998+1997-1996-1995)+(1994+1993-1992-1991)+…+(10+9-8-7)+(6+5-4-3)+2+1
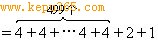
=4×499+3
=4×500-1
=1999
到此,一个繁杂的计算题,由于处理得当,思考周密精巧,加上开拓创新,很快便迎刃而解了。
