桌上放着8只茶杯。全部杯口朝上,每次翻转其中的4只,只要翻转两次,就把它们全都翻成杯口朝下。
如果将问题中的8只改为6只,每次仍然翻转其中的4只,能否经过若干次翻转把它们全部翻成杯口朝下?
请动手试验一下这时你会发现经过三次翻转就达目的。说明如下:
用±1表示杯口朝上,-1表示杯口朝下,这三次翻转过程可以简单地表示如下
初始状态+l,+l,+l,+l,+l,+l
第一次翻转-1,-1,-1,-l,+l,+1
第二次翻转+1,+1,+1,+1,-1,-1
第三次翻转-l,-l,-1,-l,-l,-1
如果再将问题中的8只改为7只,能否经过若干次翻转(每次4只)把它们全部翻成杯口朝下?
几经试验,你将发现,无法把它们全部翻成杯口朝下。
是你的“翻转”能力差,还是根本无法完成?
“±1”将告诉你:不管你翻转多少次,总是无法使这7只杯口朝下。
道理很简单。用±1表示杯口朝上,-1表示杯口朝下,问题就变成:“把7个±1每次改变其中4个的符号,若干次后能否把它们都变成-1?”考虑这7个数的乘积,由于每次都改变4个数的符号,所以它们的乘积永远不变(即永为+1),而全部杯口朝下时7个数的乘积等于-1,这是不可能的。
道理竟是如此简单,证明竟是如此巧妙,这要归功于“±l”语言。
中国象棋中的马走日字,在对弈时你发现下面这种现象没有?──
马自某个位置跳起,如果再想回到原来位置,一定经过偶次步。
±1语言也可帮你证明这个结果:
象棋盘共有9×10=90个位置,相邻位置用符号不同的数(+l与-1)来表示(图中所有实心圆点位置用+l表示,
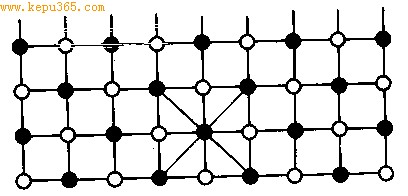
余者用-l表示),那么象棋马从任何一个位置,每走一步就要改变符号。就是说,棋子马要想不变符号,必须走偶步。而马自某个位置跳起,再回到原来位置,符号不变,故得结论:马自某个位置跳起,如果再想回到原来位置,一定经过偶次步。
