任何一样事物在推出之后,总有人会不甘于维持现状,对该事物进行改变创新,这本是无可厚非的事,如果没有这些积极寻求创新改变的人,或许现在就没有数独的存在了,它将仍是拉丁方阵的一部分,或是一些看来不具美感,难度太浅而无趣,或难度太深而失趣的数字方阵而已。
就和魔方阵一样,如果只是要人将数字1~n2填入一个n*n的方阵中,那将简单而无趣,适当的加上每行、每列及对角线的和都要相等的条件之后,难度提高了,乐趣也随之产生。
现行正规的数独,大约有如下几项要求或限制:
1.由9行、9列共81个宫格组成,并区分为九个九宫格。
2.在每一行中都要包含数字1~9。
3.在每一列中都要包含数字1~9。
4.在每一个九宫格中都要包含数字1~9。
以上三条规则,如此叙述本已足够,但有时为了加深玩者的印象,还会强调数字不可以重复;其实如果九个宫格中一定要包含数字1~9,本来就不可能重复,因为若有数字重复了,就一定会有某一个数字未被包含啊!
5.预先给定的数字必须是点对称的。
6.只有一个解。
7.必须可用逻辑的方式解题。
第1条规定了游戏的外观,第2~4条规定了游戏的规则,第5~7条则为给设计者的要求。一般而言,对第一、二项的创新修改是最容易的,对第三项的创新修改则困难多了!
另类数独
最简单的更改及创新就是将数独原本的填入物1~9换成别的对象,例如:英文字母、花草图案......等等。
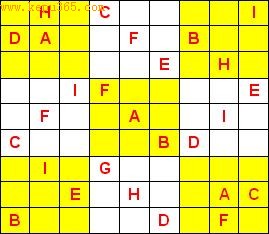
填入英文字母的另类数独
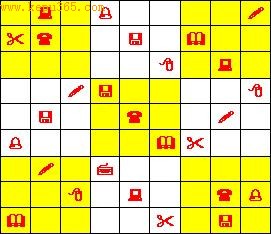
填入各种图案的另类数独
如果您真的动手去解上述二图,您将会发现:所需运用的技巧确实一点都没变,或许可以利用这点来吸引那些天生惧怕数字的人哦!
有些网站或专书为了循序渐进的理由,认为一开始就填9×9的数独,或许太难了,所以应从4×4的小数独开始入门,比较容易上手:
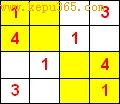
“每行、每列及每个2×2的小方阵都要包含数字1~4”的4×4数独
当然这时的填制规则也要跟着更改成“每行、每列及每个2×2的小方阵都要包含数字1~4”了。
2的平方为4、3的平方为9,4×4及9×9的数独都有了,那么下一个目标很自然的就会动到4的平方为16,也就是16×16的数独了:

“每行、每列及每个4×4的小方阵都要包含数字1~16”的16×16数独
数独的阶数由4×4、9×9到16×16,差距实在太大了,中间的阶数难道都只能被跳过而不能被使用吗?为了保有9×9数独所具有的行、列及九宫格三项限制,于是合数首先被启用了:

[1] [2] [3] 下一页
