“每行、每列及每个2×3的小方阵都要包含数字1~6”的6×6数独
只要你高兴,2×4、2×5、2×6、......3×4、3×5......等另类数独都可依类似的方式制造出来。
如果勉强要造出n×n(n为质数,亦即非合数)的数独,那这样的数独就只能有行、列的两项限制,玩起来的感觉和9×9的数独是完全不同的:

“每行、每列都要包含数字1~5”的5×5数独
当然,只要你高兴,7×7、11×1、13×13......等另类数独都可依类似的方式制造出来。
如果因为大家已习惯了9×9的数独,不想在阶数上做文章,却又想要多点创新,那么请试试武士数独吧,其填制规则,不必说明,相信您已经可猜测出来了:
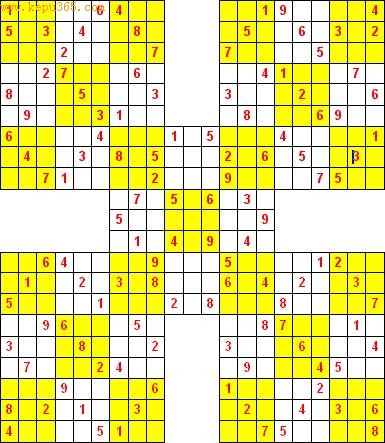
由5个9×9数独拼合的武士数独
有些人是不甘于在平面上打转的,于是创作出立体的数独来;这样的数独除了上、下方向的每一层都是3×3的数独外,侧向纵切的每一个切片也都要符合数独的条件。为了说明的方便,下面就以三阶立体数独为例吧:
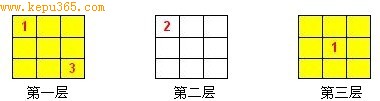
三阶立体数独的分层显示图
下面是这个三阶立体数独解的分层显示图,不论您由哪一个方向进行裁切,切割出来的3×3的方阵,都要满足数独的条件:
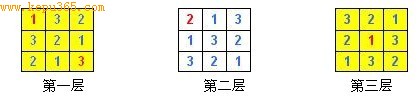
数独解的分层显示图
除了在外观上做文章之外,有些人只想在内在(填制规则)上做改变,有很多人刚看到数独时都会想到魔方阵,于是在对填制规则做改变时,很自然的就会想到套用魔方阵的规则,在原本的限制之外,再加上「在两条主对角在线也必须包含1~9」的规定,称之为“数独x”:
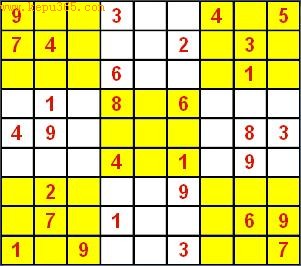
“每行、每列及每个3×3的九宫格、两条主对角线都要包含数字1~9”的4×4数独
如果没有加上「在两条主对角在线也必须包含1~9」的规定,上图的数独共有5个解,但是加上后就只有下面的唯一解了:
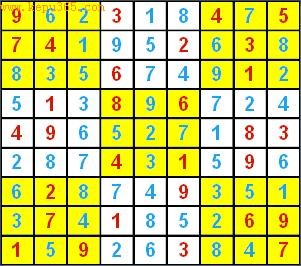
上图的数独x之唯一解
“中央数独”是另一种在
上一页 [1] [2] [3] 下一页
