填制规则上做改变的数独,除了一般数独原本的限制之外,再加上“九个九宫格的中心也必须包含1~9”的规定,称之为“中央数独centerdotsudoku”。若推广中央数独的概念,可在数独方阵中指定更多的区域一样必须包含数字1~9;例如下图的“额外群组数独ExtragroupsSudoku”除了一般数独原本的限制之外,方阵中三组不同的灰色宫格也都要包含数字1~9:

“额外群组数独ExtragroupsSudoku”
“不规则区块数独”是另一种在填制规则上做改变的数独,它舍弃了一般数独3*3的方正区块,而另外设计了每题都各不相同的不规则形状区块,由于这项改变,使得数独的阶数得以解脱,不必定要合数,所以5*5、6*6、7*7、8*8......等“不规则区块数独”都可采同样的规则限制:

9阶“不规则区块数独”
对每行、每列只能包含一个相同的数字有不同意见吗?可不可以改成都“必须包含2个相同的数字”、“必须包含3个相同的数字”、“必须包含4个相同的数字”......呢?“多次12阶数独”就是在填制规则上采取本项改变的另类数独,在12阶的方阵中,每行、每列都必须包含3个数字1~4:
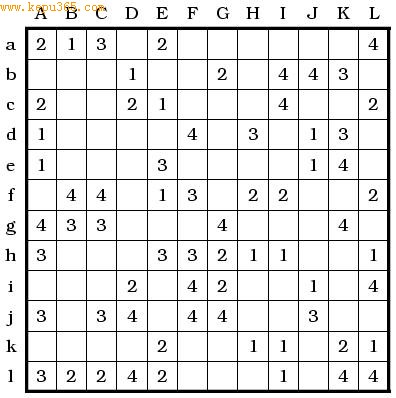
“多次12阶数独”
下面是上图的解,请参考:
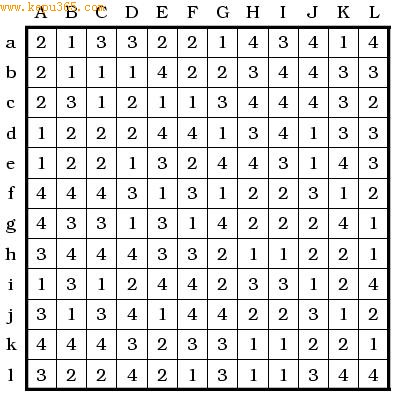
上图“多次12阶数独”之解
如果觉得数独中已给定了太多的数字,降低了它的难度,实在不够过瘾!那么就来试试“KillerSuDoku”吧!这种数独把所有给定的数字全部去除了,唯一的线索就是数个宫格串起来的方块左上角有一个数字,这个数字代表的是:“这些串起来的宫格中之数字和”,除了这点不同外,其余规定同正规的数独:
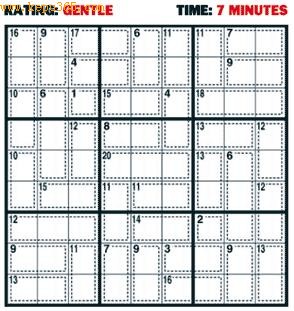
从TimesOnline上摘录的KillerSuDoku
想尝试解解看吗?附上最后的解让您参考:
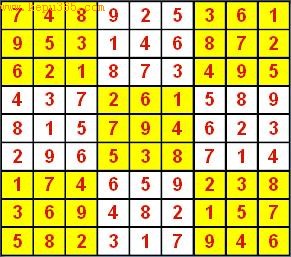
上图KillerSuDoku的解
人的想象及创造力是无限的,由一个数独竟可衍生出如此多的另类玩法。如果你想知道更多的另类数独,只要上网搜索一下,还有更多的玩法,这里就不再介绍了。
上一页 [1] [2] [3]
