在日常生活中,我们遇到的概念不外乎两类。一类是清晰的概念,对象是否属于这个概念是明确的。例如;人、自然数、正方形等等。要么是人,要么不是人、要么是自然数、要么不是自然数、要么是正方形,要么不是正方形。另一类概念对象从属的界限是模糊的,随判断人的思维而定。例如:美不美?早不早?“便宜不便宜?等等。西施是我国古代公认的美女,有道是“情人眼里出西施”,这就是说,在一些人看来未必那么美的人,在另一些人眼里,却美得可以与西施相比拟。可见,“美”与“不美”是不存在一个精确的界限的。再说“早”与“不早”,清晨五点,对于为都市“梳妆打扮”的清洁工人来说可能算是迟了,但对大多数小学生说,却是很早很早的。至于便宜不便宜,那更是随人的感觉而异了!在客观世界中,诸如上述的模糊概念要比清晰概念多得多。对于这类模糊现象,过去已有的数学模型难以适用,需要形成新的理论和方法,即在数学和模糊现象之间架起一座桥梁。它,就是我们要讲的“模糊数学”。
加速这座桥梁架设的是计算机科学的迅速发展。大家知道,人的大脑具有非凡的判别和处理模糊事物的能力。就拿一个孩子识别自己的母亲为例,即使这位母亲更换了新衣,改变了发式,她的孩子依然会从高矮、胖瘦、音容、姿态等迅速地作出准确判断。如果这件事让计算机来干,那就非得把这位母亲的身高、体重、行走速度、外形曲线等等,全都计算到小数点后的十几位,然后才能着手判断。这样的“精确”实在是事与愿违,走到了事物的反面。说不定就因为这位母亲脸上一时长了一个小疖,该部位的平均高度,比原来高了零点零几毫米,而使计算机作出“拒绝接受”的判断呢?难怪模糊数学的创始人,美国加利福尼亚大学教授、自控专家扎德(L.A.Za-deh)说:“所面对的系统越复杂,人们对它进行有意义的精确化能力就越低。”他生动地举了一个停车问题的例子,他说:要把汽车停在拥挤停车场的已有两辆汽车之间的空地上,这对有经验的司机来说,并非什么难事。但若用精确的方法求解,即使是一台大型电子计算机也不够用。
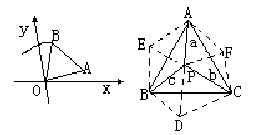
那么,要使计算机能够模仿人脑,对复杂系统进行识别和判断,出路在哪里呢?扎德教授主张从精度方面“后退”一步。他提出用隶属函数使模糊概念数学化。例如“秃头”,这显然是一种模糊概念。右图有五种头发的类型。(a)的头葫芦精光,自属标准“秃头”,隶属程度为1;(d)的头是典型的秃顶,所以“秃”的隶属程度可定为0.8;(c)的头上,长满了乌黑的头发,根本与“秃”沾不上边,所以“秃”的隶属程度为0;(b)与(c)的“秃”,比之(a)、(d)则不足,比之(c)则有余,隶属程度可分别定为0.5和0.3。这样“秃”这个模糊概念就可以用以下的方法定量地给出定义:
[秃头]=1/a+0.5/b+0/c+0.8/d+0.3/e
这里的“+”和“/”,不是通常的相加和相除。这只是一种记号。“1/a”表明状态a的隶属程度为“1”等等,“+”则表示各种情况的并列。
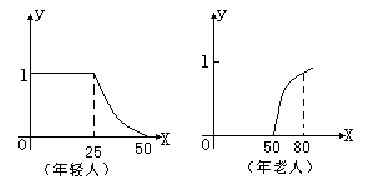
下面我们再看“年轻”和“年老”这两个模糊概念。扎德教授本人根据统计资料,拟合了这两个概念的隶属函数图象。图中横坐标表示年龄,纵坐标表示隶属程度,例如,从坐标图可以看出,50岁以下的人不属于“年老”,而当年龄超过50岁时,随着岁数的增大,“年老”的隶属程度也越来越大,“人生七十古来稀”,70岁的人“年老”的隶属程度已达94%,同样,在坐标图中我们可以看到,25岁以下的人,“年轻”的隶属程度为100%,超过25岁,“年轻”的程度越来越小。40岁已是“人到中年”,“年轻”的隶属程度只有10%。
假如有人问你:“你的数学老师年轻吗?”而你的回答却是:“他的年轻隶属程度为25%”。这样的答案自然不会有错,但显然是很别扭的。为了使人产生一种确切的印象,我们可以固定一个百分数,例如40%,隶属程度大于或等于40%的都叫“年轻”,反之就不叫“年轻”。在这种前提下,你对你朋友的回答也就是肯定的了,你可以明白地告诉你的朋友,你的数学老
[1] [2] 下一页
