,较强的一方获胜、战平、战败的频率。如下表:(单位:%)
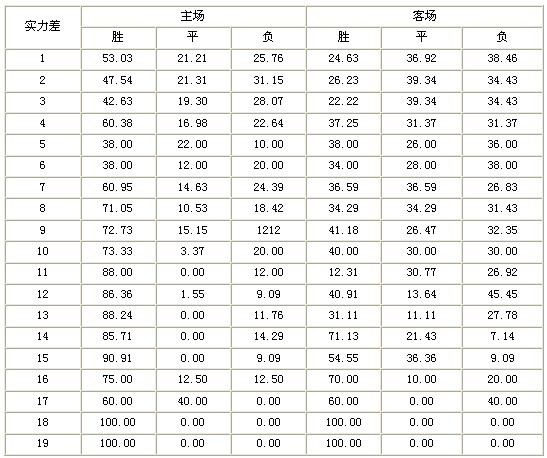
二、计算各队的理论积分
有了这些数据之后,我们可以根据求随机变量的数学期望的公式:
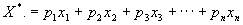
求出一支球队在同比自己实力弱的球队的比赛里的教学期望。即
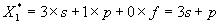
当一支球队和比自己实力强的球队比赛时,实力较强球队的战败概率就是实力较弱的球队的获胜概率。即
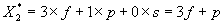
这样一来,所有比赛的数学期望都能求出。也就是说,对于每一支球队,其所有比赛数学期望值的和也能求出,我们用表示实力数i的球队的所有数学期望值的和(理论积分)。然后,将1~n这支球队对应的指从大到小依次排列成数列{},因为在世界各国的足球联赛中对降级球队数目的规定不同,有的是2支球以,有的是3支球队。根据不同的情况,只要求出数列中相应的项(保级球队中的最低分数)就是待求的理论保级分数值了。
根据这种思路,我们使用VisualBasic6.0编制一个程序来计算理论保级分数。
算法简要说明
1.输入数据:将计算所需的变量n、m通过文本框Textl、Text2输入程序中。
2.定义数组:将统计得出的s、p、f各概率值定义为三个数组s()、p()、以便赋值。再定义数列{}为一个一维数组T(20)。
3.对概率赋值:将统计得的概率数据赋至各个数组中。
4.通过循环嵌套,计算最后每支球队的理论积分,即各个数学期望之和。
5.将恰好保级的一支球队的分数输出之文本框Text3中。
具体源代码及说明(略)
运行源程序,得出下表数据:
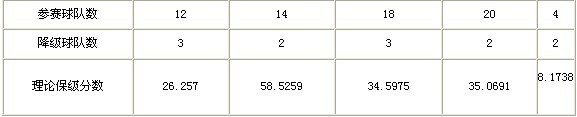
这样,一般的足球联赛都能通过这个程序求出理论保级分数。
验证模型
以上,给出了足球联赛中的理论保级分数的一种计算方法,这种方法是否理想?得出的结论能否令人满意?下面,我们通过计算值与实际值的对比,来验证这个模型。
首先,我们看2000年的甲A联赛。下表是该赛季最终的排名情况。
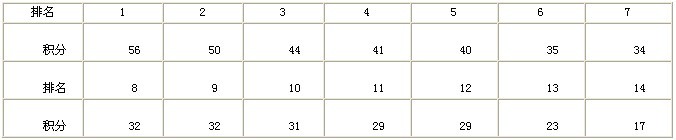
去掉两个降级球队的分数,保级分数是29分。经过上述算法,将n=14,m=2代入,计算得来的理论保级分数是28.5259分,可见,与实际保级分数相差不大。
再看看上赛季意大利足球甲级联赛,去掉3个降级的球队,实际保级分数是36分。将n=18,m=3代入,计算的理论保级分数是34.5975分,与实际情况也相差不大。
虽然用这个程序计算的保级分数有时会与实际分数有一点差距,但在大多数情况下,这个程序能够较好地估计保级分数。
上一页 [1] [2] [3] 下一页
