甲、乙、丙、丁、戊五位同学在一次数学竞赛中得了前五名。发奖前老师要他们猜一猜各人所得的名次。甲猜:乙第三名,丙第五名;乙猜:戊第四名,丁第五名;丙猜测:甲第一名,戊第四名;丁猜:丙第一名;戊猜:甲第三名,丁第四名。老师说:每个名次都有人猜对了。试问:获得第四名的是谁?
读完题目,你一定会感到头绪太多,无从下手。为了理出头绪,让我们把五位同学猜测的结果用表格列出
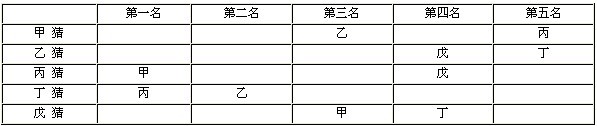
这时,注意到老师所说的“每个名次都有人猜对。”我们从表格中意外的发现:只有丁猜的“乙是第二名”这个结果是唯一的,立即可知乙一定是第二名。乙是第二名,就不会是第三名,所以甲一定是第三名。从而,甲不是第一名,则丙一定是第一名。由此又推得,丙不是第五名,丁是第五名。因为丁不可能是第四名,故第四名只能是戊。
当然,列出表格以后,根据老师所说的话,也可以从第四名是戊或丁入手。经分析,如果丁是第四名,则将引出矛盾,从而确定只能是戊获得第四名。
再举一个例子:
某次数学竞赛,共有10道选择题。评分的办法是:每一道题,答对得4分,不答得0分,答错得-1分。那么,这次竞赛至多可能出现多少种成绩。
解:我们还是根据题目的条件,列出一个得分表。
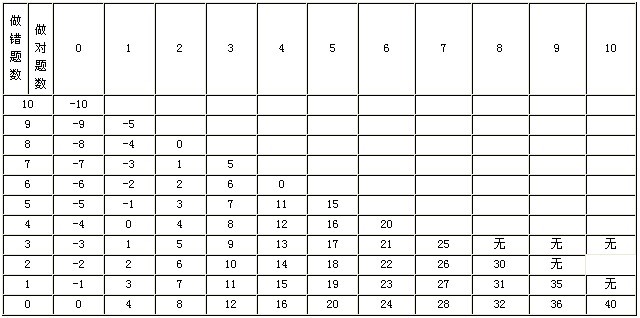
从表中立即可以看到,自-10分到-40分的五十一种分数中,不能能出现29、33、34、37、38、39六种分数。因此,这次竞赛的得分至多可能出现45种不同的成绩。
由此可知,有些问题,各种量之间关系复杂,并列出现的情况多,常会使你觉得难以入手。解题时,如果我们能选用合适的方法(包括画图、列表等),把有关的数据(或相互之间的关系)整理出来,则量与量之间的关系立刻跃然纸上,问题也就迎刃而解了。
