学夫子是一个非常喜欢“黄金分割比”的一个人,看我博客介绍就知道。在数学中,黄金分割比往往会在不经意的地方出现,比如在“欧氏对局”里面,黄金分割就是决定胜负的关键。今天给大家介绍的,是一个关于三角形的结论。
我们现在考虑各边成等比数列的三角形(a,b,c),我们会有下面的结论成立:
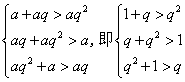
若三角形ABC的各边a,b,c成等比数列,则公比q∈(K1,K2),其中K1和K2为黄金分割比,K1=0.618……,K2=1.618……。
考虑三边a,aq,aq2,根据三角形边的关系,显然有下面的不等式成立
解这个不等式就得到k1<q<k2.黄金分割比再一次出现在我们意料之外的场合。
我们可以利用很简单的方法来证明,如果一个三角形既是等比三角形,又是直角三角形,那么必须满足公比q=√K1.当然了,如果反过来考虑的话,就把K1换成K2。
文章来源:学夫子数学博客
|
