将力分解为两反方向的无穷大力能抵消么？

这是昨日在QQ群里一位朋友提到的问题：把一个水平向右的力F分解成竖直向上和竖直向下的两个力F₁和F₂，由平行四边形法则可知，F₁和F₂都是无穷大，相互抵消了，则F也相当于不存在了。这样一来，任何一个力照此一折腾，就什么都没有了。显然从直觉讲，这是不行的，问题虽然简单，却是涉及到一些数学里比较重要的东西。

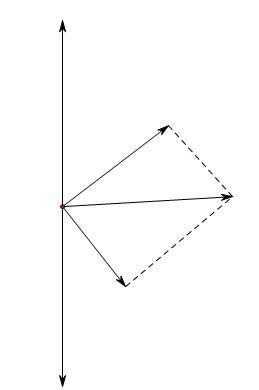
       第一个问题就是：无穷和无穷相减并不一定就是零，世间没有无穷这个数，只是一个“大得不得了”的记号而已，既然不是数，那么就不能用数字的运算法则来套用在这里。只能用极限的分析法则。你把一个力分解为两个无穷大的力，就不能简单地说他们可以相互抵消。另外一个我们若是从“射影几何”里的一个公理来看这个问题的话，会有不一样的新颖。
      两条平行直线相交于无穷远处。这就是射影几何里的一大公理。我在很多场合说过，可以把坐标轴两端看成相交于无穷远处。甚至可以把一条直线两端也看成相交于无穷远处，感觉上，一条直线就可以看成相交于无穷远处的一个圆。在数学界，很多时候都是把直线看成一种特殊的圆，比如著名的托勒密定理。所以我们可以把这两个无穷大，方向相反的力看成一个圆，他们最终相交于一点。

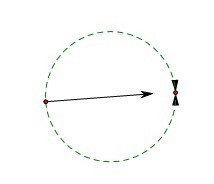
      原先向上方向的力就变成图中圆的上半圆周，向下方向的力就是下半圆周。显然，这两个力的效果最终等价于如图由起点指向重点的那一个力。而这个力正是垂直于两个无穷大力的合力。这位朋友的想法想来这也是有其中道理的，只不过不要忘记一点就是：当数进入无穷地域时，很多东西都要发生改变了，直的相当于弯的，有的相当于没有，没有的又有。
      不过这位朋友这个问题的最值得我们提到之处就是涉及到的向量基本定理。为什么一个力可以按照平行四边形法则分解为两个力？这来源于我们的向量理论，这其中的重要定理：向量基本定理。也就是平面里面任何一个向量都可以用两个不共线向量表示。而当我们分解的两个分力变成无穷大的时候，他们的方向已经共线，既然是共线，就不能成为这个平面的一组基底，向量的分解就不能在两个共线向量中进行。所以此时向量的分解，也就是这里力的分解就失效。
      文章来源：学夫子数学博客