0的0次方以及0/0

       0/0没有意义，0的0次方也没有意义，这已经是我们的常识。到了大学里面，有了“极限”这一工具，很多在我们初等数学里没有意义的东西都有了不一样的看法。没有意义的式子很多时候可以通过其极限值一窥其奥秘，关于0/0的极限情形，我已经在《为何0/0的极限值不唯一》一文里讲过，今天就来看看，为何0的0次方没有意义？其极限值有如何？
      如果我们从不同的角度看0⁰，就会得到不同的极限值，如果从0的任意次方都是0这条路，那么0⁰就应该是0，而若从任何数的0次方都等于1入手，就应该是1，从不同角度看其“取值”不一样，这便是这个式子没有意义的原因，那么其极限值又如何？实际上上面的这句话已经回答了这个问题，一个极限值为1，一个极限值为0，光从这一点就该知道，0⁰的极限值是不确定的。另外我们还可以从其他角度来看这个问题。下面的指数运算其实并不符合标准，只不过为了说明这种问题，就假设运算律适合这样的情形。
      0⁰=0^1-1=0¹/0¹=0/0，因为0/0极限值不确定，所以这个极限值不确定。有人说这种方法不对，而我则认为，这种变化恰好说明0/0的极限值不确定这一道理
      0¹=0^2-1=0²/0¹=0/0.在这种情况下，0/0就等于0，这不就恰好说明0/0的极限值不一样了吗？
      网上有很多人倾向于0/0的极限值为1的情形。一个很好的理由就是为了使得二项式定理在指数为0的时候也成立：
      (1-1)⁰=C(0,0)×1⁰×(-1)⁰=1,所以0⁰应该等于1.
      这里面就有一个问题，C(0,0)为什么等于1？如果用组合公式就会遇到0/0的情形，而这无法计算，用排列组合的定义似乎也无法解释，那你就不能说上面的式子等于1了。网络上更多人说得很悬，说是什么悬而未决的问题，搞得跟世界难题一样，这其实就是一个极限值而已，因为其极限值不唯一，所以没有确定值。

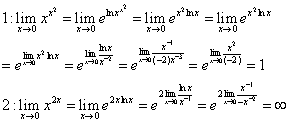
文章来源：学夫子数学博客