数学里的与时俱进思想 |
|
|
| 来源:不详 更新时间:2012-1-8 21:06:44 |
|
|
|
|
数学是在发展的,对于数学的整个历史进程来说的话,很多方面都能够带给我们很多的启示,大家还记得数学史上的三次数学危机吧!为什么会产生数学危机,无非就是由于新的事物带来了许多思想观念上的冲击,很多人承受不了这种打击,再加上新思想的不成熟,碰撞在所难免,这一碰撞,就不仅仅是唇枪舌剑,往往还付出生命的代价。以一个简单的例子来说说,与时俱进是多么的重要。
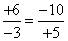
这个式子或许在我们看来没有什么东西可说吧,上过初中的都知道。不过在“负数”出现的那个时代,却有很多问题让数学家们头疼不已,上面的式子其实反映了下面一个道理:
大数:小数=小数:大数
这个问题在当时是无法理解的,一个大的数和一个小的数的比值,怎么可能和一个小的数与大数的比值相等?如果有朋友对现在的这个问题还有所迟疑的话,说明还没有把握住数学里的核心思想。另外一个有意思的问题,其核心之处和上面一样:

这个问题也是负数刚出现时,很多保守派提出的一个景点问题。在我们没有接触负数这个概念以前,我们有“分子不变,分母越小,则分数越大”这样的结论,如果把这个结论放在这里的话就会出现可笑的矛盾。1/(-3)有多大呢?如果分子保持1不变,那么分母越小,其值越大,当分母小到“0”的时候,这个分数就是无穷大,而现在出现负数了,说明分母就比0还要小,这么说,1/(-3)不是比无穷大还要大吗?这算什么呢?
现在我们都知道,出现这样的问题,其实是没有注意到,“分子不变,分母越小,则分数越大”这个法则,只适合于正数的情况,对于负数根本不适合。而这样的事实其实给我们最大的启示就是,对待新事物,不可用已有的旧观念去看待,新事物,就一定要有新观念,这样才不至于闹笑话,我们往往觉得和老一辈有隔阂,就是如此。
文章来源:学夫子数学博客
|
上一个数学: 初等数学里的那几个“链式法则”
下一个数学: 勾股数组的快速构造 |
|
|
|
|
