将一个数分解为几个数之和,使之乘积最大 |
|
|
| 来源:不详 更新时间:2012-2-8 11:30:08 |
|
|
|
|
这是一道经典,又是容易犯错的题目。因为涉及到神秘的e,所以给这道题也增加了几分新鲜感。原题是这样的:有几个数之和为19,问这几个数的最大乘积为多少?这里是限制在正实数范围内。当然,这里的19可以是代替为任何数。不过不管是什么数,都有下面统一的答案:
当每一个数都相等,且每一个数都非常接近于e的时候,其乘积最大。
对于19而言,将之分解成7份的时候,每一个数19/7离e(2.71828……)最接近,也就是这几个数的最大乘积为(19/7)7.对于这个答案的证明,需要一点导数知识,不过都是非常基础的。利用均值不等式,可以知道当每一个数都相等的时候,才具有最大值,所以实际上就是将这个数均分,假设分成n份,那么他们的乘积就是:(k/n)n.其中k为这几个数的和,为一常量。利用导数知识,可以算出其极值点。
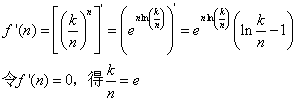
由此便有了答案,其中的k/n就是分解出的每一个数,不过当我们在均分的时候,k/n就不一定能取到e了,因为此时的n限制在了正整数的范围,根据f(n)的单调性,当每一个数最接近于e的时候,其乘积最大。
比如把12分解成几个正数之和,当每一个数都等于3的时候,他们的乘积最大,我们也可以通过简单的验证来检验。又比如3,不用分解,就他一个数的乘积最大。这个问题属于一道非常常见的题目,不过往往很多人犯一些错误,最容易犯错的地方就是将“正实数”随意拓展为“一切实数”。实际上就拿19来说,一个简单的验证就知道“一切实数”内是可以到达任何大的。
1019+(-500)+(-500)=19,显然此三数的乘积远比(19/7)7大得多。
文章来源:学夫子数学博客
|
上一个数学: 数学启示之团队“忠与患”
下一个数学: 你的出生年加上你的年龄都等于2012! |
|
|
|
|
