作者:学夫子
为什么是负负为正?这里的题目说得很清楚,其实就是一种规定。当然这种规定是建立在深刻的数学背景下的,而不是某个人的突发奇想。一门数学学科都是建立在“公理——定理”的基础上的,算术也不例外,算术的公理,就是一系列的运算法则,这些法则无法证明,他的建立基本上都是建立在直觉的基础上。有人试图对负负为正作出证明,显然这是徒劳的。他们提供的证明方法如下,看起来没有破绽,实则漏洞百出。
证明负负为正:
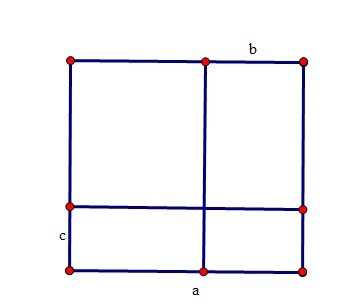
图中的图形就是一个边长为a的正方形,根据面积公式必然有下面的式子成立:
(a-b)(a-c)=a2-ac-ab+bc………………①
然后不知道为什么的,他就让a=0,根据上面的式子得到(-b)(-c)=bc,从而就认为证明了"负负为正"的结论.看起来似乎很有理呢!实际上是完全错误的,因为①式之所以成立,前提是建立在a≥c的前提下的,既然前提都不同,又怎么可以突破这个前提得出其他的结论呢?本来这里面是有很多东西需要讨论的,这样一"证明"一下子就将之变得显而易见了.但是这种不按照规矩办事,想当然滴将结论扩大的思想是绝对不行的.他会给学生造成一种错误的印象,这种印象无论是对于研究还是生活都是有非常大的危害.因为在这里想当然滴将条件放宽,自以为得到正确的结论,那么学生就容易在诸如下面的问题犯错:
正数范围有分母越大,分数越小的结论,但是显然加了负数以后就不成立.很多例子都告诉我们,当条件变化,很多结论都会变,所以利用上面的思想来解释负负为正,绝对是要不得的.
不过上面错误的方法却可以给我们得出下面的结论。我们通过面积得到了式子①。实际上就是关于乘法的结合律问题。实际上就是得到了在正数范围内多项式的一个运算法则。现在我们引进了负数,要想使得这些运算法则也能够适用于负数,也就是让负数“兼容”这些运算法则的话,就必须要负负为正,上面错误的做法已经说明了这一点。
而恰好,如果赋予负数以几何意义——反方向的话,也必须要“负负为正”,因为反方向的反方向就是正方向。综合这些,就顺理成章滴需要规定“负负为正”的公理。但是你不能用他们去证明负负为正,这是无法证明的,他属于最底层的公理。
换句话说,如果你愿意,你可以规定“负负为负”,但是这种规定不兼容正数的运算法则,会带来很大的麻烦。(来源:学夫子数学博客)
