作者:学夫子
基本上来说,题目可以大致说明今天的内容,那就是说说三角形的重心性质与物理学里的“杠杆原理”之间的联系。用数学研究物理学已经是众所周知,但是用物理学研究数学问题却不多见,这是一个很好的例子,算是作为一个开头,到后面我将逐步写一些用物理学原理研究数学问题的实例,一定能给我们不一样的感觉,这会让你感觉数学并非死板的公式,很多还是物理定律的反映。
首先我们必须知道今天的两个主角——重心性质和杠杆原理。
杠杆原理:
质点组的重心在两质点的连线上,且到两质点的距离与这两点的质量成反比。用图形话的语言来说就是:
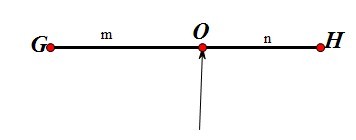
如图所示,两个质点G和H的质量为G和H,其平衡点为O,G到O点的距离为m,H到O点的距离为n,则必有Gm=Hn
重心性质:
三角形ABC的平衡点是三条中线的交点,且中点分每一天中线成2比1的比例:
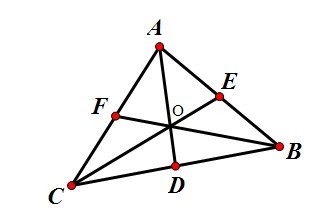
现在我们就要用杠杆原理来证明重心性质。我们在A、B、C三点放置质量为单位1的质点,因为A和B的中点为E,所以A和B的质量就等于聚集到了E点,说明A、B、C三点的重心一定在直线CE上,同理也在AD和BF上,进而证明O点就是三角形ABC的平衡点,其实也间接证明三线共点。现在我们来证明第二个性质。
因为D是BC的中点,所以D点就相当于拥有了2个质量(B和C的总和),根据杠杆原理有:
M(A)×AO=M(D)×DO。从而AO/DO=2,其中M(A)代表质点A的质量.
这便揭示了三角形重心原理的物理本质,原来就是著名的杠杆平衡原理.其实,数学中的很多性质都从不同方面反映了物理学定律.比如向量,因为力是一种向量,所以有关于向量的很多结论其实都可以看作是力学原理在数学上的推广.有时候还会反映出电学,光学等性质,比如折射定律,其实就是数学里的最小值问题,反过来,光的很多性质可以用来解决数学中的最值原理.这一现象正好说明数学来源于自然超越于自然的特征。(来源:学夫子数学博客)
|
