作者:学夫子
当我无力快速解决某题目时候,暴力成为了最后的堡垒。有时候还来得非常完美。比如下面这道著名的数学游戏,出自于著名数学游戏玩家赫柴德,他与20世纪中期征求下面字谜算式的答案:(其中相同的字母代表相同的数字,不同的字母代表不同的数字)

可能很多人都会认为答案有很多个,但结果令人惊讶,满足条件的式子只有下面一个,不过据说其演算还比较复杂,最后是由一位数学爱好者用计算机运行11分钟完成。学夫子闲下来的时候,就试着用暴力解决此题,下面是我的爆破过程,比较无聊,阅读宜谨慎。
1:首先,两个一位数相乘保持末尾数不变的本就不多,而两位数ON与一位数B相乘保持末尾两位为ON的就更少了,满足条件的就下面几对,显然B=1和0的应该排除,如果排除掉N=0的情况,那么剩下的就更少:(25,9);(75,9)。我们下面的任务就是排除这两种情况而证明数字N只能为零。
A:此时B=9,那么D*9不能向后进位,否则千位上的N*9不可能末尾数仍然是5,符合条件的D只有0和1.简单验证便知D只能为0,因为若D=1,D*9同样会产生进位。若O=2,D=0,则S=2,重复;所以在这种情况下,O只能为7
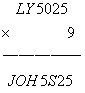 _____________ _____________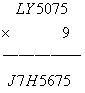
如右图就是当O=7时候的算式,该算的都已经计算出来了,此时Y只能取1,2,3,4,8几数之一,一个一个试。
(1):若Y=1,则H=3,Y*9进1,L*9+1的个位数为7,则L=4,J=6,重复;
(2):若Y=2,则H=2,重复;
(3):若Y=3,则H=1,Y*9进3,L*9+3的个位数为7,则L=6,重复;
(4):若Y=4,则H=0,重复;
(5):若Y=8,则H=6,重复。
如此演算得知,N只能为0.
B:N=0时,O*B就需要保持末尾数不变,符合此题要求的有下面几对:(3,5),(7,5),(9,5),(6,2),(6,4),(6,8),爆破法的精髓即将用上:

(1):当O=5,B=7或9,则D只能为零,否则就会向N*B进位,而这就与N=0重复。
(1):当O=5,B=3.D*B不能进位,则D只能为1或2,否则D*3就会向后进位。
i:当D=1或2,此时Y可以取1,2,6,7,8,9之一
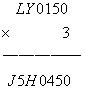
a:当Y=1或2,Y*3不能向后进位,而L*3的个位数为5,所以L=5,重复
b:若Y=6,则H=8,Y*3向后进1,L*3+1的个位数为5,则L=8,重复
c:若Y=7或8或9,则H=1或4或7,Y*3向后进2,L*3+2个位数为5,则L=1,如此便不能进位得到J
d:若Y=4,则H=2,Y*3向后进1,L*3+1的个位数为5,则L=8,J便为2.与H重复。
(3):若O=2,B=6,同样的道理,D=1.此时的Y只能取3,4,5,8,9之一
[1] [2] 下一页
|
