如果对海伦公式求导 |
|
|
| 来源:不详 更新时间:2012-4-27 13:03:56 |
|
|
|
|
作者:学夫子
乘着昨天的文章,我就想着无聊地对一些数学公式求导,我想到了海伦公式,于是海伦公式又被我折腾了。
海伦公式是一个已知三角形三边求三角形面积的著名公式,以其美妙的结论流传于世

现在如果我们以c为自变量,对S(c)求导的话,会有什么结果?当然,其中p是关于c的函数,所以需要将之换成另外的一种形式
f(c)=√(a+b+c)(a+b-c)(a-b+c)(-a+b+c)/4
=√((a+b)2-c2)(c2-(a-b)2)/4
现在对f(c)求导,得到:
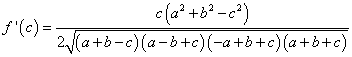
好了,我看到了,好像没有什么值得探究的,很乱的嘛。没有昨天我们所讲的球体积公式对半径的导数是面积,圆面积公式对半径的导数是圆周长那么漂亮,不过还是有一点值得我们注意:那就是当导数值为零的时候,a2+b2-c2=0,这是什么?勾股定理啊!
为什么f'(c)取零的时候,三角形刚好就是直角三角形?除了我们通过上面的公式得出以外,我们有必要找一个直观化的说明。那就先要明白导数取零点时候的几何意义:当导数值为零的时候,原函数取到极值点。虽然极值不一定是最值,不过在这里我们可以这样说。于是这个问题转化为:为何当三角形面积取最大值时,该三角形为直角三角形?
在这里就需要请出另外一个三角形面积公式:S=1/2absinα,相信各位都很熟悉的吧!既然在前面我们对f(c)求导,显然我们就必须把a和b当成常数,当a和b固定不变的时候,唯有当sinα=1也就是α=90°的时候,三角形面积取得最大值。
由此便解释f'(c)等于零时为什么三角形是直角三角形。(来源:学夫子数学博客)
|
上一个数学: 用数学方法来做文学作品的鉴别
下一个数学: 一道趣味代数题 |
|
|
|
|
|
|
