圆的一个有趣性质 |
|
|
| 来源:不详 更新时间:2012-4-27 13:10:38 |
|
|
|
|
作者:学夫子
对于圆的定义,我想就不用我说,今天所说的这个,是圆的一个性质,但是这个性质和圆锥曲线非常类似,而正如我们所知道的,圆可以看做是一种特殊的不得了的椭圆,所以个人经常把他看做圆的定义,虽然这个非常不妥。
定理:和两已知点的距离之比等于常数(不等于1)的点的轨迹是一个圆周。
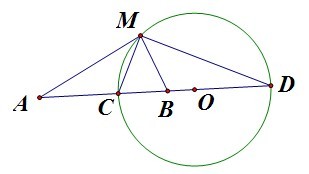
设A、B为已知点,求点M的轨迹,使得比MA/MB为一不等于1的常数m。
显然C点是一点,MA/MB=AC/CB,利用“角平分线定理”的逆定理知,MC为角AMB的角平分线。而MD外分线段AB,DA/DB=MA/MB,可以知道MD平分角AMB的外角。这个性质可以利用三角形相似以及三角形的面积公式证得。在此先忽略,各位若对此有问题的话,可以留言,如果有必要,我单独起文说明。
由此可以知道,角CMD=90°,所以M点在圆周上。
这个定义是不是和圆锥曲线的定义很相似?圆锥曲线的定义是到定点和定直线的距离之比为一常数,而这个是到两个顶点的距离之比为一常数。从另外一个角度看,我们还可以看出一些其余的端倪:
如果这个比值为1,那么M的轨迹就是AB的垂直平分线,如果比值不为1,那就是一个圆。也就是说,线段在这里可以看成当圆的半径趋于无穷大时候的极限情况。这个看似荒唐的结论其实非常重要,在比较复杂的数学理论里,往往是把直线看成一种特殊圆的,在这里很难说清楚,不过有一个例子可以一窥其妙,那就是托勒密定理。大家可以参考这篇文章:<托勒密定理探究>,也可以参考维基百科的一些资料:关于托勒密定理。(来源:学夫子数学博客)
|
上一个数学: 关于连续自然数的k次方和
下一个数学: 从韦达定理反推一元二次方程判别式 |
|
|
|
|
