作者:学夫子
我们知道,在圆锥曲线里,要数椭圆和双曲线两兄弟关系最好,这方面在我们前面的文章已经有所提及。如果我们来重新审视椭圆和双曲线的定义,便有了不一样的想法.
椭圆:到两定点的距离之和为一常数的点的轨迹
双曲线:到两定点的距离之差为一常数的点的轨迹
好事的学夫子学到这的时候,自然而然就想到:加和减都有了,乘和除会是怎样?也就是说,我们给出下面的问题:
1:求到两定点的距离之比是一常数的点的轨迹
2:求到两定点的距离之积是一常数的点的轨迹
我们先看第一个问题
1:这个问题我已经在《圆的一个有趣性质——类似于圆锥曲线》一文里给出了解答。
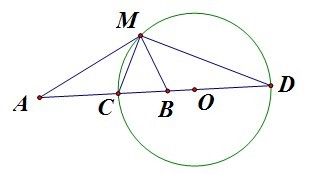
如图所示,A、B为定点,M到A和B的距离之比为k,如果k=1,那么M的轨迹为线段AB的中垂线,如果k≠1,那么M的轨迹为一个圆。这个结论运用解析法就很容易解决,具体就请自己试试,或者参考文章《圆的一个有趣性质》。
现在我们来看第二个问题,也是今天的精彩之处
解:我们借助处理圆锥曲线的办法,设两个定点的坐标为A(-a,0)好B(a,0),设动点M=(x,y),M到A和B的距离之和为b2(为何如此设?后面就会明白),利用两点之间的距离公式,然后进行一系列化简,将得到下面的方程式:
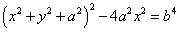
这是一个什么图像的方程?我们以前没有见过,我在这里先告诉你们答案:这个图像的形状取决于k=b/a的比值,当k>1,轨迹是一条封闭曲线;当k<1,轨迹是两条不相连的封闭曲线;当k=1.图像是一条双纽线,就像一个躺着的8字。下面的动画展示了这样的图像,右上角的k值就是b/a的值。这个曲线叫做卡西尼卵形线
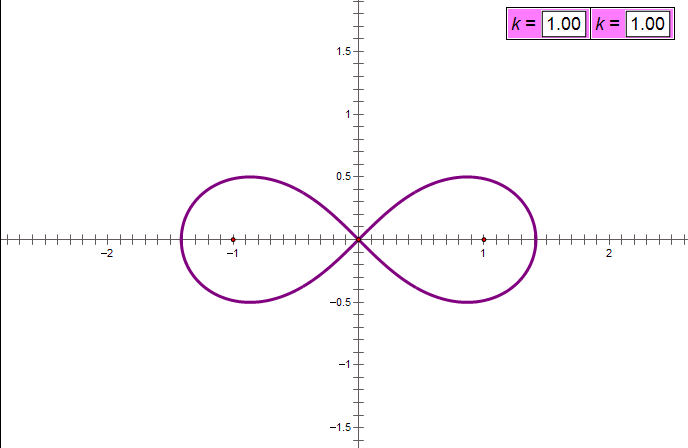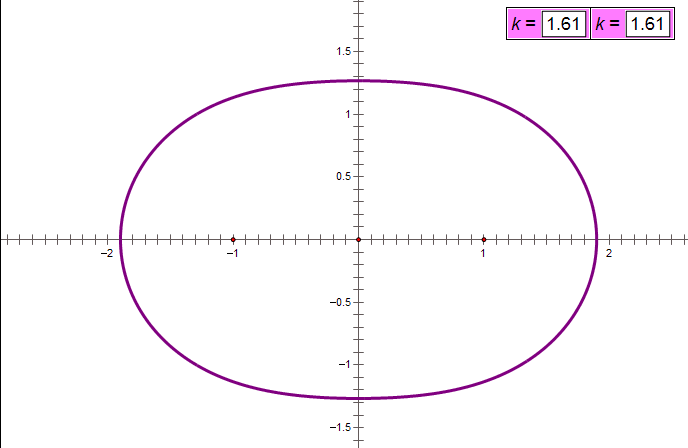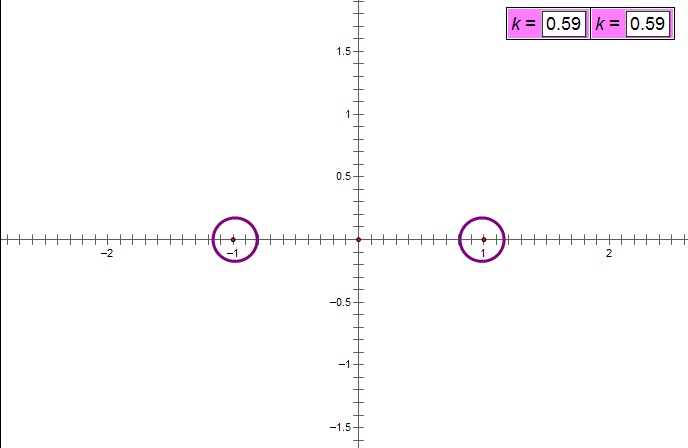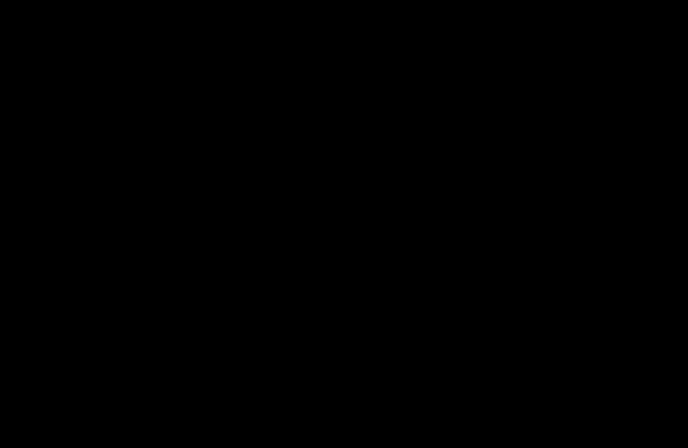
来源:学夫子数学博客
|
