面积的一个定义法 |
|
|
| 来源:不详 更新时间:2012-5-22 12:21:34 |
|
|
|
|
作者:学夫子
我们或许再也熟悉不过,矩形面积为长宽乘积,三角形面积为底乘高的一半,那么有没有想过,到底什么是面积?这个问题又很多说法,比较靠谱的说法就是,将边长为1的正方形的面积定义为1,由这个定义得出正方形长方形面积,进而得出平行四边形、三角形面积公式等等,包括微积分里面的封闭图形的面积,也是如此。不过,今天我们从另一个角度来看待这个问题,那就是我们从三角形的面积公式说起。
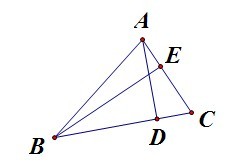
上面的三角形中,AD和BE是三角形两条边上的高,我们可以通过相似三角形的原理得到下面的性质:
三角形的底边与高的乘积是一常数,只与三角形本身有关,而与所选的底边无关。
证明:在直角三角形ADC和BEC中,他们有一个公共角C,所以这两个直角三角形相似,所以有
AC/BC=AD/BE,也就是BC×AD=AC×BE。得证。
由此,我们把这个乘积与某一个常数k的乘积称为三角形的面积。而对于k的取值,我们一旦确定以后就不再变更,那么这个k应该如何取?为此,我们就要做一些规定,k的取值必须使得边长为1的正方形的面积为1.
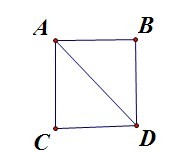
正方形可以分割成两个直角三角形,S=k+k=1,所以k=1/2.为了使得边长为1的正方形的面积为1。k就应该取1/2.所以我们有了三角形的面积公式:
S=1/2底×高。
有些很简单的问题,当我们从另一个角度思考的时候,往往会有不同的发现。就如同三角形的面积公式一样,又有谁想过:为什么三条底边与高的乘积始终是一致的?(来源:学夫子数学博客)
|
上一个数学: 道路着色问题
下一个数学: 三角形和四面体 |
|
|
|
|
