作者:学夫子
学夫子题记:很久以前写过两篇文章——《数学启示之亦正亦“斜”》和《再说三人正则后人正》,收到的反响很不错。有兴趣的朋友可以去看看,大体内容就是:以任意一个三角形的三边为边长做三个正三角形(不管是向内还是向外),这三个正三角形的内心恰好是另一个正三角形的顶点。另外一个就是关于莫利定理
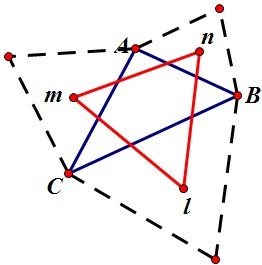
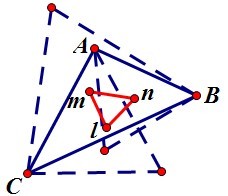

时隔一年半光景,学夫子收到迄今为止最精彩的反馈,一位名叫“千里草”的前辈,给学夫子提供了许多非常珍贵的建议,在此表示感谢。现在将这位前辈的想法发于此,希望得到大家的支持。(来信稍有修改)
我们知道任意一个三角形都有着许多伴随着他的正三角形。如果我们进一步想:由于是任意三角形,那么对于不同形状的三角形,做莫利三角形、拿破仑(外)三角形、拿破仑(内)三角形,三种模式各会出现什么情况?其中的许多道道,细细品味起来还非常有意思。为了说明问题,下面的图都是按照等比例绘制,以便观察
一:适用于莫利三角形
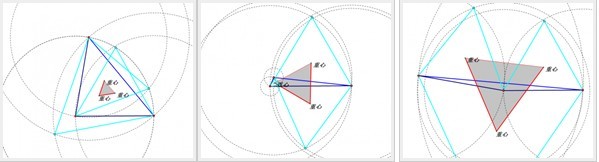
1:三条边长度差距不大的三角形

2:当三条边的长度差距越大,观察中间莫利三角形的大小变化


我们通过观察可以得出一些比较感性粗糙的结论:在保持其中一条边长度不变的情况下,当三角形三条边的尺度差异越大,三角形本身的形状越不均衡,“心中”的正三角形就会变得越小。不过,即使三角形再怎么畸形,只要他还是个三角形,心中的正三角形依然存在。这也正是现实生活中,对人性最浅显和公正的写照——每个人心中都有正义,当一个人本身变得扭曲不规整,心中的“正义”就会变得越发渺小,甚至小得无法看见。但是,正义依然存在,放下屠刀依然有成佛余地。
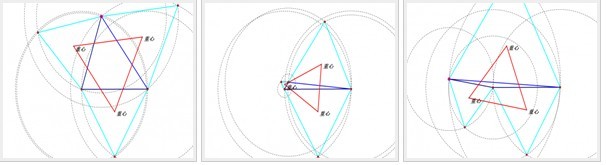
二:适用于拿破仑(内)三角形
与莫利三角形不同,这种三角形的结果恰好与莫利三角形相反:当三角形三条边长度差异越大,得到的拿破仑内三角形越小,反之越大。如果将莫利三角形看成一个人心中故有的正义,那么拿破仑内三角形就是一个人(三角形)对自身的内省。或者是对自身的一种反省,那些在我们眼中看起来歪歪斜斜的人或事,却往往用于转化为正面因素的巨大的、不可想象的潜力。相反,看起来规规矩矩之人,又如各方面都很优秀或者都不优秀的人,如果是单纯的自我内省,也不会有多大的提升空间了。佛曰:大恶会转化为大善。也许你不是全才,但是只要你善于同自己交流,时刻自我内省,以此基础创造出的价值,远比所谓的全才来得激烈,
三:适用于拿破仑(外)三角形
前面的结果是,莫利三角形随着三角形的不规整越来越小,拿破仑内三角形随着三角形的不规整而变大。拿破仑外三角形填补其中空白——不管三角形怎么变,他的大小都不会发生大的变化。
[1] [2] 下一页
