蜜蜂们……依靠某种几何学上的预见……知道六边形大于正方形和三角形,可以用同样一些材料储存更多的蜜。
——亚历山大的帕帕斯
蜜蜂没有学过镶嵌理论,圆形织网蛛也没有学过对数螺线。但是正像自然界中的许多事物一样,昆虫和兽类的建筑常常可用数学方法进行分析。自然界用的是最有效的形式——只需花费最少能量和材料的形式。不正是这一点把自然界和数学联系起来的吗?自然界掌握了求解极大极小问题、线性代数问题和求出含约束问题最优解的艺术。
把我们的注意力集中于蜜蜂,可以观察到许多数学概念。
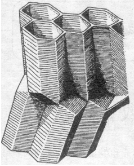
正方形、正三角形和正六边形是仅有的三种自镶嵌正多边形。其中,对于给定面积来说,六边形的周长最小。这意味着蜜蜂在建筑蜂房中的六角柱巢室时,比起用以正方形或三角形为底的棱柱来镶嵌空间的情况,可以用较少的蜡和做较少的工作围出相同的空间。蜂房的壁由大约1/80英寸(英制长度单位,1英寸合2.54厘米。——译者注)厚的巢室壁构成,但能支持自身重量的30倍。这就是蜂房给人以沉重感觉的原因。大约14.5英寸×8.8英寸的蜂房能储存5磅多的蜜,而建筑所需的蜡只有大约1.5盎司(英制重量单位,1盎司合28.3495克。——译者注)。蜜蜂用三个斜棱柱截段构成六角柱,巢室壁交接处恰巧成120°角。蜜蜂们同时在不同截段上工作,天衣无缝地筑成一个蜂房。蜂房是垂直向下建筑的,蜜蜂把它们的部分身体用作测量仪器。事实上,它们的头起着测锤的作用。
蜜蜂所拥有的另一迷人的“工具”是“罗盘”。蜜蜂的定向受到地球磁场的影响。它们能探测到地球磁场中只有灵敏磁强计才能辨别的微小涨落。这就是为什么一群蜜蜂在占据一个新的地点时可以在这新领域的不同部分同时开始建筑蜂房而并无任何蜜蜂领导着它们的原因。所有蜜蜂都按照与旧蜂房相同的方向为它们的新蜂房取向。
在下页图中,可见巢室排得很紧密,蜜蜂已经用半菱形十二面体将端处盖好。此外,蜜蜂所建室壁的斜度是13°,这样可以防止蜂蜜在端顶被蜡帽封盖前流出。
通信联络是又一个令人感兴趣的领域。工蜂经过长途侦察回到蜂房时,以“跳舞”的形式发出一串代码,表明它们找到的食物源的方向。它们能传达食物的方向和距离。跳舞相对于太阳的定向提示食物的方向,跳舞的持续时间则指出距离。同样令人惊奇的是,蜜蜂“知道”两点之间的最短距离是一条直线。或许这是“蜂线”(beeline,即两点之间的直线。——译者注)这一术语的可能来源。工蜂在花间随意来去而采集到大量花蜜后,它知道取最直接的路线回到蜂房。蜜蜂是通过它的遗传密码获得数学训练的。从数学的观点分析自然界的各个方面,是一件有趣的事情。对于蜜蜂生活的这一瞥也不例外。我们在这里发现了材料和工作的最优化、平面和空间的镶嵌图案、六边形、六角柱、菱形十二面体、几何定理、磁场、代码和惊人的工程技术。(文章来源:中小学教育网)
